NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Leyes de Newton, dinámica del movimiento circular)
|
|

|
 |
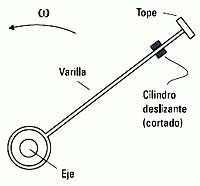
FIS 53 - La varilla de la figura se hace girar con
velocidad constante en un plano vertical. La misma
tiene un tope a 90 cm del eje, y por ella desliza
un cilindro pequeño, de 200 g. Puede despreciarse
la masa de la varilla y el rozamiento sobre
el cilindro. |
|
|
a- Si realiza una vuelta por segundo, calcular
la intensidad de la fuerza que el tope hace sobre
el cilindro, en los puntos más alto y más bajo de
la trayectoria, respectivamente.
b- Hallar cuál será la máxima velocidad que
puede dársele, si la varilla soporta una fuerza de
tracción máxima de 20 Newton.
c- Hallar la mínima velocidad con que podrá
girar, sin que el cilindro se separe del tope. |
 |
|
|
|
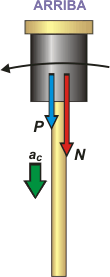
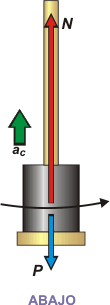
En muchos ejercicios de movimiento circular, incluido éste, en el que el movimiento transcurre en un plano vertical, se plantean interrogantes que tienen que ver con dos posiciones críticas: la posición inferior y la posición superior. En ambas, las fuerzas que actúan son verticales. No siempre, pero en muchas.
Después vuelvo a discutir por qué esas dos posiciones son críticas. Por ahora me voy a conformar con que hagamos los DCL para ambas posiciones, la de arriba y la de abajo. |
|
 |
Habrás leído bien que el movimiento de la varilla es constante. Eso facilita las cosas. Porque entonces la aceleración (centrípeta, obviamente) también va a ser constante, y la calcularemos de cualquiera de estas dos formas
ac = ω². R = v² / R
según nos convenga.
Fijate que una vuelta por segundo equivale a una velocidad angular de ω = 2π s-1. La ecuación de Newton dirá:
ΣF = m aC
N + P = m . ω² . R (ARRIBA)
N — P = m . ω² . R (ABAJO)
donde lo único que puede cambiar entre una situación y la otra es la fuerza que hace el tope, N. Todo lo demás es constante. ¿Está claro? |
 |
|
|
(ARRIBA) N = m ( ω² . R — g )
N = 0,2 kg ( (2π s-1)² . 0,9 m — 10 m/s² )
|
|
| |
NARR = 5,1 N |
respuesta a- |
|
|
(ABAJO) N = m ( ω² . R + g )
N = 0,2 kg ((2π s-1)² . 0,9 m + 10 m/s² )
|
|
|
| |
NABJ = 9,1 N |
respuesta a- |
|
|
|
Según podés ver en estos resultados (seguramente ya lo habías razonado antes, la fuerza normal que hace el tope es mayor abajo. Luego si ahora le ponemos un valor máximo, NMAX, (que si lo supera se rompe) ese valor debe alcanzarlo abajo, y no arriba ni en ninguna otra posición, de modo que, nuevamente...
(ABAJO) NMAX — P = m . vMAX²/ R
vMAX² = R (NMAX — P) / m
vMAX² = 0,9 m (20 N — 2 N ) / 0,2 kg
|
|
|
| |
vMAX = 9 m/s |
respuesta b- |
|
|
|
Por último, al disminuir la velocidad disminuye la sumatoria de fuerzas, o sea, disminuye la fuerza que hace el tope, porque el peso no puede variar, ¿estamos de acuerdo? Cuando nos dicen sin que se separen el tope y el cilindro equivale a decir que la fuerza normal mínima valga 0,000000000000000...1 N (es un modo infantil de decirlo, pero aclara un poco la situación). Lo que nos interesa es la situación límite... que la fuerza hace el tope valga cero. ¿Dónde podría ocurrir tan singular fenómeno? Arriba de todo, claro.
(ARRIBA) P = m . vmín²/ R
vmín² = R P / m = R g
vmín² = 0,9 m . 10 m/s²
|
|
Las barras de fracción han de dibujarse horizontales.
En NO ME SALEN aparecen oblicuas por las razones explicadas
acá. |
|
| |
vmín = 3 m/s |
respuesta c- |
|
|
|
| DISCUSION: Estas situaciones críticas, o singulares, en las que una de las variables del problema alcanza un máximo, o un mínimo, o se anula, o se iguala con otra, o le pasa algo significativo representan situaciones notables sobre las que suelen hacer preguntas los ejercicios. Habitualmente no te describen toda la situación sino que dejan parte de la interpretación a cargo tuyo, y dependerá de vos que aciertes a entender qué te están preguntando. Por eso es súper importante que entiendas la mecánica de los sistemas, cómo funcionan, qué le pasa a los cuerpos mientras el sistema está en marcha. Esa comprensión del universo no cabe en un machete. |
|
 |
| DESAFIO: ¿Cuánto vale la fuerza que hace el tope en la posición 30, 90 y 150 grados con la vertical, cuando la barra se mueve a ω = 2π s-1? |
|
| Agradezco a Jonathan Bossio que detectó un error en uno de los resultados. Algunos derechos reservados.
Se permite su reproducción citando al autor, anotá: Ricardo Cabrera, ¿me tenés?. Última actualización dic-06. Buenos Aires, Argentina. |
|
|
|

