 |
NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Leyes de Newton, dinámica del movimiento circular)
|
|

|
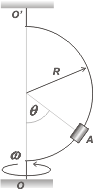
NMS d3.01 -Un cilindro A puede deslizarse libremente a lo largo de una barra lisa corvada en un semianillo de radio R, según el gráfico. El sistema se hace girar alrededor del eje vertical OO´ a la velocidad angular constante ω. Determine el ángulo θ correspondiente a la posición estable del cilindro.
Este hermoso ejercicio tiene una "trampa exquisita": un dispositivo terriblemente sofisticado que esconde un problema muy sencillo. Se trata de un péndulo cónico común y silvestre, como el que resolvimos varias veces (acá tenés un ejemplo) y en el que el piolín del péndulo está reemplazado por una barra circular. Si todavía no te diste cuenta, no te preocupes, abajo lo describo con detalle. |
 |
|
Como todo ejercicio de dinámica (comprendas o no comprendas el dispositivo) tenemos que empezar por un DCL. Acá va: |
|
|
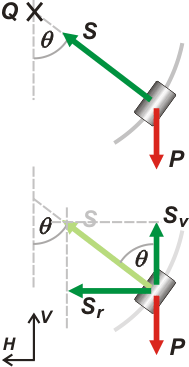 |
Sobre el cilindro actúan sólo dos fuerzas: su peso, P, claro está, que es vertical. Y la fuerza que hace el anillo, S, que, como el enunciado indica que puede deslizarse libremente, eso quiere decir que no puede hacer fuerzas tangenciales (rozamiento) y sólo puede hacer fuerzas radiales. De modo que S tiene la dirección de un radio del anillo, apunta hacia el centro del semianillo, Q.
O sea, el semianillo hace una fuerza idéntica a la que haría un piolín fijo al punto en el centro del anillo. Estamos frente a un péndulo cónico disfrazado, ¡atado con un piolín invisible!
Como las fuerzas no son codireccionales, elegimos un sistema de referencia (vertical-horizontal) y descomponemos la fuerza S.
SV = S . cos Θ
SH = S . sen Θ |
|
|
|
Ahora sí, vamos a Newton. En el eje vertical tenemos que la aceleración es cero (el manguito no cambia de altura). Y en el eje horizontal, tenemos un MCU.
ΣFV = 0 → SV — P = 0 → SV = m . g [1]
ΣFH = m ac → SH = m ac → Sc = m . ω² . r [2]
|
|
|
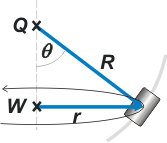 |
Pero acá hay que hacer una advertencia (no son pocos los que caen en ese error). El radio de giro, r, del manguito NO ES el mismo que el radio del semianillo, R. (Sólo serían iguales si Θ valiese 90 grados). El manguito gira en una circunferencia horizontal con centro en W.
Por suerte hay una relación sencilla entre ambos:
r = R sen Θ
|
|
|
|
Ya casi llegamos: juntemos todo lo que sabemos en las ecuaciones [1] y [2].
S . cos Θ = m . g
S . sen Θ = m . ω² . R sen Θ
En la segunda ecuación podemos cancelar sen Θ. Luego, si dividimos miembro a miembro las dos ecuaciones, obtenemos:
cos Θ = g / ω² . R
De donde: |
|
|
|
|
|
En criollo: Θ es el ángulo cuyo coseno vale (g/ω²R).
DISCUSION: Lo primero que me fijo cuando obtengo un resultado es si las unidades son las que corresponde. En efecto el paréntesis (g/ω²R) es un adimensional -sin unidades- lo que es correcto para una función trigonométrica. Lo segundo es pensar si tiene sentido físico... ¡y lo tiene! Fijate: la función coseno varía entre 0 y 1. Valdrá 0 cuando Θ valga 90 grados, y 1 cuando Θ valga 0 grado. Si la gravedad fuese mayor al manguito le costaría más subir por el semianillo (luego el coseno de Θ sería más grande y Θ más chico). En cambio si ω² o el radio del semianillo, R, fuesen más grandes, también lo sería Θ. Pensalo por separado... a mí me cierra.
OBSERVACIÓN: en algunos escritos la expresión arc tg, o la operación inversa de cualquier función trigonométrica, suele escribirse como una potencia -1 de la función directa. No es correcto, ya que no es cierto que la función inversa sea igual a la inversa multiplicativa. Se trata de una deformación de notación que surge de limitaciones tecnológicas. Pero es bueno estar atentos. cos-1 α no es lo mismo que arc cos α. |
|
 |
| DESAFIO: Describir dinámicamente la independencia de la masa que nos arroja el resultado. (No algebraica... una explicación dinámica). Buscar en cualquier enciclopedia, o en INTERNET, el regulador de watt, y encontrarle alguna relación con este ejercicio. |
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Última actualización
oct-11. Buenos Aires, Argentina. |
|
|
|

