 |
NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Leyes de Newton, dinámica del movimiento circular, péndulo cónico)
|
|

|
NMS d3.05- Se hace girar un objeto mediante una
cuerda de 0,5 m de longitud, atada al techo en el
extremo libre, de modo que la cuerda forma un ángulo constante de 37° con la vertical (péndulo
cónico). Calcular el período del movimiento circular
uniforme que describe el objeto. Analizar si
dependerá de su masa. Realizar la experiencia y
verificar el resultado. Analizar qué valor tiene el
período, para un ángulo menor que 5°.
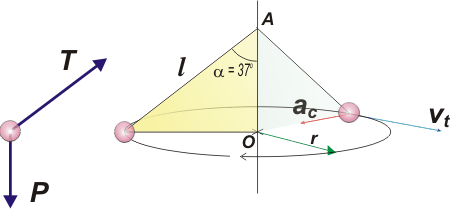
Como siempre, hay que arrancar con un DCL, pero también voy a hacer un esquemita del péndulo que creo que te va a ayudar y seguro que lo usaremos durante la resolución del ejercicio. |
 |
|
|
Bueno, acá está el DCL, describiendo las dos únicas fuerzas que actúan sobre el péndulo cuando se halla en la misma posición que te lo dibujé en el esquemita. La fuerzas son; el peso de la masa, P; y la tensión con que lo tira la cuerda, T.
Cosas destacables del esquema. La circunferencia que describe el péndulo es horizontal y tiene su centro en O (¡no en A!), y su radio r. En una posición -de cuando viaja por atrás- aproveché y te dibujé un vector aceleración centrípeta, ac , y una velocidad tangencial, vT , ¿te cierra todo? Bueno, tenemos que escribir las ecuaciones de Newton, pero, como las fuerzas no son co-direccionales, debemos descomponer una de ellas. Lo más práctico es descomponer T. Acá va de nuevo el DCL. |
|
|
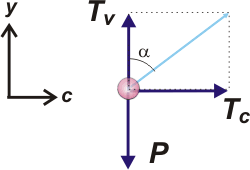 |
Recordás que siempre que enfrentás un MCU a uno de los ejes lo llamás c (por centrípeto), en lugar de x, ¿no? Es cierto que se trata de un eje que va cambiando con el tiempo. Pero no te olvides que la dinámica son sólo instantáneas del universo. Fijate que α = 37º y eso permite establecer que
TV = T . cos α
Tc = T . sen α |
|
|
|
| Ahora sí, vamos a Newton. En el eje vertical tenemos que la aceleración es cero (la circunferencia no cambia de altura). |
|
|
| |
ΣFy = 0 |
→ |
TV — P = 0 |
→ |
TV = m . g |
[1] |
|
| |
ΣFc = m ac |
→ |
Tc = m ac |
→ |
Tc = m 4π² . r / T² |
[2] |
|
|
|
|
Como el enunciado nos hace preguntas sobre el período, elegí reemplazar la aceleración centrípeta por alguna de aquellas expresiones que contienen T. Pero todavía falta mucho, no te apures. Vamos a hacer así: vamos a reemplazar las componentes de la tensión por su igual expresado en función del ángulo α,
T . sen α = m 4π² . r / T²
T . cos α = m . g
y vamos a dividir miembro a miembro la [2] con la [1]. Así se cancela la tensión, cuya T se confunde con la de período (pero fijate que no son iguales)...
T² . sen α / cos α = 4π² . r / g [3]
También se canceló la masa, lo cual no es menor: indica que el período es independiente de la masa. Ahora esto: r no es dato del problema, pero tené presente que lo puedo reemplazar por l y α, qué sí son datos. Para eso mirá el triangulito amarillo que dejé a propósito en el esquema.
r = l . sen α
reeemplazo esto en [3]
T² . sen α / cos α = 4π² . l . sen α /g
sen α multiplica en ambos miembros, puede volar. El coseno lo paso multiplicando al segundo miembro así dejo solito al período.
T² = 4π2 cos α . l /g
Raíz cuadrada en ambos miembros...
T = 2π ( cos α . l /g )½
|
|
 |
| |
T = 1,27 s |
independiente de la masa |
|
|
|
Sabés que cualquier cosa elevada a la potencia 1/2 es lo mismo que raíz cuadrada de esa cosa... ¿no es cieto? Bueno para inclinaciones con la vertical menores que 5 grados... qué ocurre.
cos 5º vale 0,9962 y (cos 5º)½ vale 0,9981, o sea, valores extremadamente cercanos a 1 y que en la multiplicación afectan recién al 3er o 4to decimal. Para ángulo menores a 5º la cercanía con 1 aumenta. La cuestión es que solemos despreciar ese factor, y entonces, a los fines prácticos, la ecuación del período queda... |
|
|
|
|
|
DISCUSION: Vamos a discutir sobre esta última expresión que recuadré en amarillo, que por otro lado es la más popular. Verificá primero que tenga las unidades correctas... ¿en qué se medían los períodos? Bueno... dá. La expresión dice que ¡el período de oscilación del péndulo depende exclusivamente del largo del hilo! Y lógicamente, que es mayor cuanto más largo sea éste. Las otras cosas que intervienen son constantes... no modifican el período... sólo el hilo.
Un péndulo ideal, el más común de todos, el que usa el hipnotizador, tiene una dinámica no tan sencilla como la del péndulo cónico. Lo interesante es que el resultado, después de mucho batallar, es el mismo para ambos. |
|
 |
| DESAFIO: ¿Qué largo tiene la cuerda de la que cuelga el péndulo gigante en la planta baja del pabellón II de Ciudad Universitaria? Si te interesa el asunto podés visitar este sitio que queda muy cerca: péndulo. |
|
| Algunos derechos, zurdos y ambidiestros reservados.
Se permite su reproducción citando la fuente. De los ambidiestros también. Última actualización oct-06. Buenos Aires, Argentina. |
|
|
|

