| |
NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
Rozamiento |
|
|

|
| |
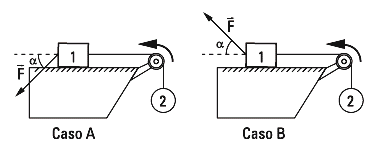
d2.36 - Para las dos situaciones planteadas en la
figura, donde la intensidad de F es la misma en
ambos casos, determinar cuál de los sistemas
adquiere mayor aceleración (¿o es la misma?) si
inicialmente se mueven en el sentido indicado.
Justificar sin hacer los cálculos.
|
|
| Datos: m1 = 10 kg; m2 = 6 kg; μd = 0,25;
|F| = 40 N; α = 37° |
|
|
Uy... estamos fritos... el enunciado pide que respondamos y justifiquemos la respuesta sin hacer cálculos. Qué problema... Bueno, no hay que angustiarse, no es tan difícil como parece. Hay quien lo logra y quien no... pero para llegar a eso no sólo hace falta buena intuición, hacen falta horas de vuelo, es decir, haber resuelto muchos ejercicios de dinámica.
Hagamos una cosa: resolvamos el ejercicio como lo hacemos usualmente y al final discutimos el asunto de la resolución sin cálculos.
Vamos a la primera situación (caso A) y los DCL correspondientes. |
|
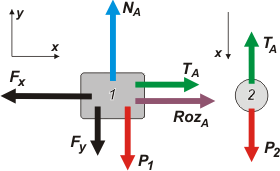 |
Te habrás fijado que los DCL que hice no son los verdaderos, si no los útiles, es decir ya tienen un SR elegido, y que la única fuerza que no coincide con ese SR ya está descompuesta el las direcciones útiles.
Fijate también que el sentido del eje x es coherente entre ambos cuerpos. Ojo.
También fijate que el sentido del rozamiento (en este caso un deslizamiento) es contrario al sentido del movimiento que indica el enunciado. |
|
|
Hechas todas las aclaraciones, vamos a resolver la primera parte del ejercicio. Este es el set de ecuaciones de Newton.
bloque 1, eje x → TA + RozA — Fx = m1 . aA
bloque 1, eje y → NA — Fy — P1 = 0
bola 2, eje x → P2 — TA = m2 . aA
Además, sabemos que la fuerza de rozamiento dinámica, en este caso vale:
rozamiento din. → RozA = μd . NA
Juntando las cuatro ecuaciones podés despejar la aceleración del sistema. Esta vez no lo voy a hacer, porque estoy seguro de que sos capaz. Si necesitaras ayuda algebraica tenés un caso muy parecido en el ejercicio 1.34. |
|
| |
aA = (P2 + μd P1 + μd Fy — Fx )/ (m1 + m2) |
respuesta no numérica |
|
|
| |
aA = 3,69 m/s² |
respuesta exacta |
|
ver nota |
| El valor positivo de la aceleración (que indica un sentido contrario al del movimiento) indica que el sistema se está frenando. Vamos al Caso B. |
|
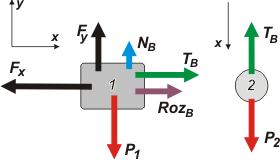 |
Prestale mucha atención a las diferencias con el anterior par de DCLs.
El apoyo, NB, es menor que antes, ya que ahora hay una fuerza nueva que ahora tira para arriba y que antes tiraba para abajo, Fy.
Por lo tanto también podemos anticipar que entre los rozamientos encontraremos que RozA > RozB. |
|
|
Las nuevas ecuaciones de Newton son:
bloque 1, eje x → TB + RozB — Fx = m1 . aB
bloque 1, eje y → NB + Fy — P1= 0
bola 2, eje x → P2 — TB = m2 . aB
Además, sabemos que la fuerza de rozamiento dinámica, en este caso vale:
rozamiento din. → RozB = μd . NB
Nuevamente, juntando las cuatro ecuaciones, podés despejar la aceleración del sistema. |
| si vos sos de los que se resisten a usar subíndices... estás en la lona |
|
| |
aB = (P2 + μd P1 — μd Fy — Fx )/ (m1 + m2) |
respuesta no numérica |
|
|
| |
aB = 2,94 m/s² |
respuesta exacta |
|
|
| |
|
| |
Con lo cual podemos afirmar que aA > aB. Pero discutamos el caso.
Primero: no es evidente que el cuerpo se esté frenando, eso no se puede resolver intuitivamente, ya que hay que comparar qué fuerzas son más grandes; si las que tiran para la derecha (Roz y P2) o la que tira para la izquierda (Fx).
Segundo: es un poco más evidente que el rozamiento es máyor en el primer caso, porque el cuerpo está más apretado contra el piso, pero eso no resuelve el caso anterior, en el que el resultado del ejercicio sería el contrario.
Tercero: si llegaste a las mismas respuestas (no numéricas) que yo (intentalo), y las comparás, se ve claramente la diferencia que hay en el numerador. Son idénticas, salvo que en el caso A hay un término sumando y ese mismo término está restando en el caso B. La conclusión es obvia.
O sea: me parece que el autor de este ejercicio se pasó de rosca.
Nota: para realizar el cálculo numérico tenés que saber que Fx = F cos α y también que Fy = F sen α. (Vos ya lo sabías, perdón). |
|
 |
| DESAFIO: ¿Cuánto vale la tensión de la soga en cada caso? ¿Cuál sería la respuesta a este ejercicio (la relación entre aceleraciones) si la masa de B valiese 20 kg? |
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. El Comité Internacional de Pedadogos Constructivistas ha resuelto prohibir la utilización de este material didáctico, desde ahora debes hacerlo en forma clandestina. Agradezco a Daniel Calisti por el envío de una errata. Última actualización
dic-10. Buenos Aires, Argentina. |
|
|
|

