NO ME SALEN
EJERCICIOS RESUELTOS DE FÍSICA DEL CBC
(plano inclinado, rozamiento)
|
|

|
| NMS d2.23 - Un cuerpo de masa M es subido a velocidad constante por un plano inclinado a través de una soga paralela al plano. En el trayecto actua una fuerza de rozamiento constante cuyo módulo es igual al 20% del peso. Si la inclinación del plano respecto a la horizontal es de 37°, ¿cuánto vale la fuerza que se ejerce a través de la soga? |
|
Veamos qué pasa. Lo primero de lo primero, como en todos los ejercicios de dinámica es empezar por el DCL.
|
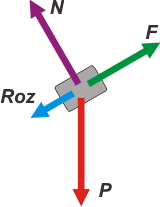 |
Las fuerzas que actúan sobre el cuerpo son 4. Su propio peso, P; la fuerza con que lo sostiene el plano, N; la fuerza de rozamiento, Roz, que debe apuntar hacia abajo ya que el cuerpo está subiendo; y la fuerza incógnita con que tira la soga hacia arriba, F.
Vamos a necesitar 2 ecuaciones de Newton, ya que las fuerzas no son co-direccionales y además vamos a tener que elegir e indicar un sistema de referencia. |
|
|
|
En base al SR indicado, descomponemos la fuerza que no coincide con ninguno de los dos ejes: |
|
|
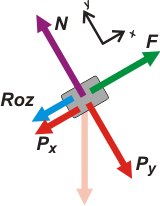 |
Así aparece:
Px = P . sen 37º
Py = P . cos 37º
(Si no entendés cómo realicé esa descomposición de la fuerza peso, podés verlo acá).
Vamos a usar estos valores redondeados:
sen 37º = 0,6
cos 37º = 0,8
|
|
|
| Si no sabés cómo se descompone la fuerza peso y cómo obtener el valor de las componentes, podés verlo acá. |
|
Y como el cuerpo sube a velocidad constante, la aceleración vale 0. Las ecuaciones de Newton quedan así:
ΣFx = 0 → — Roz — P . 0,6 + F = 0
ΣFy = 0 → N — P . 0,8 = 0
La segunda ecuación no aporta gran cosa. Pero la primera nos va a resolver el ejercicio. Acordate que el enunciado nos da un dato interesante: el rozamiento es igual al 20% del peso. Si lo reemplazamos ahí, nos queda:
— 0,2 P — 0,6 P + F = 0
De donde:
F = 0,8 . P
Y para responder en los términos del enunciado: |
|
|
|
|
|
|
|
|
| DESAFIO: ¿Qué cambiaría si la masa aumentase al doble? |
|
 |
| Algunos derechos reservados.
Agradezco a José Velásquez por el envío de una errata. Se permite tu reproducción recitando en la fuente. Última actualización may-13. Buenos Aires, Argentina. |
|
|
|

