NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Leyes de Newton, cuerpos vinculados, plano inclinado, rozamiento)
|
|

|
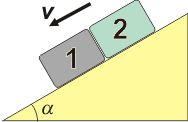
NMS d2.22*- Los bloques 1 y 2 cuya masa son m1 y m2 se deslizan hacia abajo sobre un plano inclinado un ángulo α como se muestra en la figura. El bloque 2 está apoyado sobre el 1. Los coeficientes de rozamiento entre los bloques y el plano inclinado valen μ1 y μ2 respectivamente. Hallar la fuerza de contacto entre los bloques. Posibles respuestas:
|
|
a- (μ1— μ2) (g sen α/m1 — m2) m1 . m2
b- (μ1— μ2) (g cos α/m1 + m2) m1 . m2
c- (μ1— μ2) (g tg α/m1 + m2) m1
d- (μ1— μ2) (g /m1 + m2) m1
e- (μ1— μ2) ( m1 . m2 sen α/m1 + m2)
|
 |
|
|
Este ejercicio es muy original en el sentido de que los coeficientes de rozamientos de los bloques con el plano son diferentes. Éso y sólo éso hace que aparezca una fuerza de contacto distinta de cero entre los bloques. Y está muy claro: si el bloque 1 está más frenado que el bloque 2 por efecto del rozamiento, el 2 se apoya en el 1, como indica el enunciado. Ese apoyo lo llamaremos F12 o F21, indistintamente, ya que son los pares de interacción que aparecen sobre cada bloque por efecto de la misma interacción: el contacto mutuo.
Hago los DCL y los comentamos. |
|
|
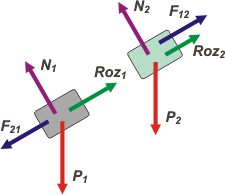 |
Estos DCLs son fundamentales si tu objetivo es entender la dinámica del sistema. Te muestra las interacciones de cada uno de los cuerpos.
Sobre el bloque 1 actúan cuatro fuerzas: su propio peso, P1; el apoyo en el plano, N1; su rozamiento con el plano, Roz1; y la fuerza de contacto con el bloque 2, F21.
Sobre el bloque 2 actúan también cuatro fuerzas: su propio peso, P2; el apoyo en el plano, N2; su rozamiento con el plano, Roz2; y la fuerza de contacto con el bloque 1, F12. |
|
|
|
| Ahora, para resolver el ejercicio necesitamos que los DCLs sean operativos, es decir, que las fuerzas que muestran apunten en direcciones ortogonales e independientes -x e y- que permitan operar algebraicamente. Elegimos un SR y descomponemos algunas fuerzas. |
|
|
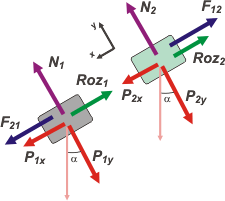 |
Cualquier SR hubiera servido... pero éste, cuya dirección x coincide con la dirección y sentido de la aceleración, y que coincide en direcciones con seis de las ocho fuerzas que teníamos... va a ser el más sencillo y económico.
Descomponemos las dos fuerzas que no coinciden con las direcciones x e y, y de ahí nos vamos a las ecuaciones. No te olvides que para cada cuerpo:
P1x = m1 . g . sen α
P1y = m1 . g . cos α
|
|
|
Si en un examen te olvidás de identificar el SR con el que vas a trabajar, tu docente te va a bajar 2 puntos y vos no vas a poder decir ni mu. |
P2x = m2 . g . sen α
P2y = m2 . g . cos α
Bueno basta de cháchara, vamos a resolver el ejercicio. Este es el set de ecuaciones de Newton. No te olvides que los bloques bajan juntos, en contacto, de modo que la aceleración de ambos es la misma. |
|
|
| |
bloque 1, eje x |
→ |
F21 + P1x — Roz1 |
|
= m1 . a |
[1] |
| |
bloque 1, eje y |
→ |
N1 — P1y |
|
= 0 |
[2] |
| |
bloque 2, eje x |
→ |
— F12 + P2x — Roz2 |
|
= m2 . a |
[3] |
| |
bloque 2, eje y |
→ |
N2 — P2y |
|
= 0 |
[4] |
| Y además agregamos una ecuación para cada bloque que describe la naturaleza del rozamiento: |
| |
bloque 1 |
→ |
Roz1 |
|
= μ1 . N1 |
[5] |
| |
bloque 2 |
→ |
Roz2 |
|
= μ2 . N2 |
[6] |
|
|
|
El ejercicio ya está cocinado. El resto es álgebra y tenés 447 caminos diferentes para explorar. Acá hagamos así: despejamos la aceleración de las ecuaciones [1] y [3].
a = (F21 + P1x — Roz1) / m1
a = (— F12 + P2x — Roz2) / m2
Reemplazo los rozamientos ([5] y [6]) y los componentes de los pesos:
a = (F21 + m1 . g . sen α — μ1 . N1) / m1
a = (— F12 + m2 . g . sen α — μ2 . N2) / m2
Idem con los apoyos con el plano ([2] y [4]):
a = (F21 + m1 . g . sen α — μ1 . m1 . g . cos α) / m1
a = (— F12 + m2 . g . sen α — μ2 . m2 . g . cos α) / m2
Simplifico un poco:
a = (F21 / m1) + g . sen α — μ1 . g . cos α
a = — (F12 / m2) + g . sen α — μ2 . g . cos α
Desde ahora a las fuerzas de contacto las voy a llamar directamente F. Igualo las dos ecuaciones y cancelo el término que aparece en ambos:
(F / m1) — μ1 . g . cos α = — (F / m2) — μ2 . g . cos α
Reordeno:
(F / m1) + (F / m2 ) = μ1 . g . cos α — μ2 . g . cos α
En el primer miembro hago la suma de fracciones y en el segundo saco factor común:
F (m1 + m2) / (m1 . m2 ) = (μ1— μ2) g . cos α
|
|
|
| |
F = (μ1— μ2) (g cos α / m1 + m2) m1 . m2 |
respuesta b) |
|
|
|
| El resultado es muy razonable. Tratá de discutirlo un poco. Acá te presento algunas preguntas posibles: ¿qué pasaría si α valiese cero?, ¿qué pasaría si los coeficientes de rozamiento fueran iguales?, ¿qué pasaría si alguna de las masas fueran despreciables? (Casi que analizando el resultado lo podría haber elegido de entrada sin hacer ninguna cuenta). |
|
|
| *Este ejercicio pertenece al Curso de Admisión UNI, Lima, Perú, 2012, y me fue enviado por mi amigo José Velásquez. |
|
|
|
| |
|
|
| |
|
 |
| DESAFIO: ¿Cuánto vale la aceleración de los bloques? |
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Última actualización oct-12. Buenos Aires, Argentina. |
|
|
|

