 |
NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Leyes de Newton)
|
|

|
No me salen d2.16* - Un cuerpo desliza con velocidad constante sobre un plano inclinado 10°. ¿Cuánto valdrá su aceleración deslizando sobre el mismo plano inclinado 20°?
Este es un ejercicio muy bonito gracias a la economía de datos. Tenemos dos situaciones para pensar y relacionar: la primera sobre un plano inclinado 10° y la segunda sobre el mismo plano, pero ahora inclinado 20°. La clave del asunto para entender la primera situación es la frase del enunciado: velocidad constante.
El único modo el en que puede ocurrir eso es que al menos una fuerza exterior esté actuando sobre el cuerpo compensando el tirón hacia abajo que provee el peso. Una candidata excelente para ese cometido es la fuerza de rozamiento. Acá va el DCL, entonces, para esta primera situación.
|
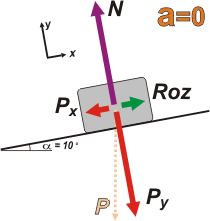 |
Tenés una situación idéntica descripta en el ejercicio 2.6. De todos modos es muy sencilla. La fuerza peso, P, ya la muestro descompuesta en las dos direcciones ortogonales x e y. Tené en cuenta que:
Px = P sen 10º
Py = P cos 10º
La naturaleza de la fuerza de roce y la 2da. Ley de Newton nos ofrecen tres ecuaciones. Son éstas: |
|
|
|
El rozamiento → Roz = μd . N [1]
En el eje x → Roz — Px = 0 [2]
En el eje y → N — Py = 0 [3]
Combinándolas llegamos a una expresión de que es lo único que no cambia (además de la masa del cuerpo) entre una situación y la otra. Se puede hacer así: reemplazo la [1] en la [2]...
μd . N — Px = 0
Ahora la [3]...
μd . Py — Px = 0
μd . P cos 10º = P sen 10º
μd = tg 10º
Si podés hacer el esfuerzo de no reemplazar esa expresión por su equivalente numérico... quiere decir que estás madurando. Vamos a la segunda situación: el mismo cuerpo, el mismo plano, pero inclinado 20°... |
|
|
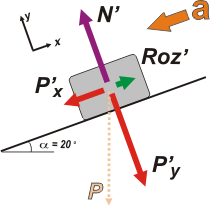 |
Como ves, la cosa es muy parecida a la anterior... ¡pero cambian los valores de todas las fuerzas que nos interesan! Por eso les puse nombre diferente. Supongo que entenderás por qué -aunque el peso vale lo mismo- Px es menor que P'x , y lo inverso ocurre con la componente perpendicular al plano... Y si seguís el razonamiento, el nuevo apoyo, N', es menor que en la situación anterior... Y por lo tanto el rozamiento también disminuyó, y el equilibrio se ha roto.
Tené en cuenta que:
P'x = P sen 20º
P'y = P cos 20º
|
|
|
|
Por lo tanto ahora tenemos una aceleración distinta de cero... pero que podemos averiguar. El planteo es el mismo:
El rozamiento → Roz' = μd . N' [4]
En el eje x → Roz' — P'x = m . a [5]
En el eje y → N' — P'y = 0 [6]
Meto la [4] y la [6] en la [5], y me queda esto:
μd . P'y — P'x = m . a
Reemplazo los pesos por su equivalente (mg), cancelo la masa que multiplica en todos los términos... y despejo la aceleración:
a = g . ( μd . cos 20º — sen 20º )
El coeficiente de rozamiento es el mismo de antes, ya que las superficies que rozan son las mismas... no interesa en qué ángulo respecto de la vertical estén rozando... luego:
a = g . ( tg 10º . cos 20º — sen 20º )
|
|
|
|
|
|
Es cierto que a este razonamiento arribamos suponiendo lo del rozamiento, y que de no ser así no hubiésemos podido resolverlo... La justificación es la siguiente: se trata de la única suposición posible para que la pregunta sea contestable. Con eso basta. Y como si fuera poco: es la situación física más plausible, común, simple... ¿te hablé alguna vez de la navaja de Ockham? |
|
|
*Este interesante ejercicio me lo envió María Florencia Grenier.
|
|
 |
DESAFIO: ¿En qué porcentaje disminuyó la fuerza de rozamiento? |
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Lo que dice en la siguiente oración es falso. Lo que dice en la oración anterior es verdadero. Última actualización feb-09. Buenos Aires, Argentina. |
|
|

