NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
|
|

|
dN2.5- Se debe construir una cinta transportadora
para elevar cajas de cartón. La inclinación de
la cinta es 30° y las cajas pesan 30 kgf. Se dispone
de tres materiales para hacer la cinta:
|
tela plástica : µe = 0,4 ; µd = 0,3
lona: µe = 0,6 ; µd = 0,4
goma: µe = 0,8 ; µd =0,5
|
 |
|
|
Elija el material que resultaría más adecuado,
teniendo en cuenta que la goma es más cara que
la lona y ésta que la tela plástica. Justifique.
Calcule la fuerza de rozamiento que actúa sobre
la caja mientras está subiendo e indique claramente
su sentido. ¿Se podrá usar la cinta para
transportar cajas del mismo material pero de distinto
peso? (Para todas las consideraciones necesarias
suponga que las cajas se depositan en la
cinta ya en movimiento y que no deben soportar
frenadas ni aceleraciones). |
|
Me imagino que alguna vez viste una cinta transportadora. Es como una escalera mecánica, pero no para personas sino para cajas. Las cajas van inclinadas, de modo que si no hubiese rozamiento las cajas no sólo no podrían subir sino que deslizarían y caerían a la vereda y después andá a reclamar que en el cartón decía claramente "frágil".
La cinta transportadora, creo, es el más hermoso ejemplo de que la fuerza de rozamiento no necesariamente se opone al movimiento y muchas más veces que lo que pensamos va a favor del movimiento, que se produce GRACIAS y no A PESAR del rozamiento. Tenelo presente, y vamos ya mismo al DCL. |
 |
|
|
|
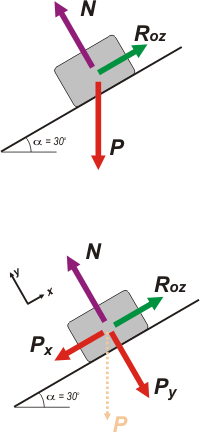
Acá lo tenés. Actúan sobre la caja, cada vez que depositamos una sobre la cinta sólo tres fuerzas. No hace falta siquiera que te las mencione.
Está claro que si la cinta fuese de un material poco rugoso, y con el lustre que mi abuela le aplicaba al piso del comedor no serviría de nada. Pero tampoco necesitamos comprar un material súper rugoso porque es más caro y dura menos. Acá hay un compromiso, entonces lo que vamos a hacer es buscar un límite, un mínimo necesario para que la fuerza de rozamiento se banque las cajas de 30 kg sin que se le escapen. Le vamos a permitir a ese material que use su rozamiento máximo del que sea capaz, cosa que logra cuando:
RozeM = μe . N [1]
Las tres fuerzas no son codireccionales, de modo que descompuse una de ellas, el peso,
Px = P sen 30º
Py = P cos 30º
Estás de acuerdo, ¿no? |
|
|
Bueno, si estás de acuerdo, vamos a las ecuaciones de Newton para los dos ejes. Y no te olvides que si la velocidad es constante (todas las cintas transportadoras importadas y nacionales trabajan a velocidad constante) la aceleración es nula.
En el eje x → Roz — Px = 0 [2]
En el eje y → N — Py = 0 [3]
Ya está, si contas cuántas incógnitas hay vas a llegar a 3. De modo que esto tiene solución algebraica. ¿Lo hacés solo? Ok, ya entendí. Reemplazamos la ecuación [2] y la [3] en la [1], queda así:
P sen 30º = μe . P cos 30º
sen 30º = μe . cos 30º
μe = tg 30º = 0,577
|
|
| |
habría que comprar lona, μe Lona > 0,577 |
|
|
|
Ahora prestá mucha atención a ésto: Para calcular la fuerza de rozamiento no siempre se encuentra aplicando RozeM = μe . N . El 63,35% de los estudiantes cometen ese error (garrafal si lo hacen durante un examen). La fuerza de rozamiento estático es una fuerza variable. Sus valores puede ir desde cero hasta un valor tope, máximo, en cada situación. En el 99% de los casos no estamos en el máximo. Acá la condición es que la caja no deslice, o sea, que su aceleración valga cero. Eso ya lo está diciendo la ecuación [2]
Roz = m . g . sen 30º
|
|
|
|
|
| |
|
 |
| DESAFIO: Mi pregunta es ésta, (no tenés que calcular nada... pero tenés que pensar lo suficiente...) si al tener velocidad constante la aceleración vale cero... ¿por qué no las ponen a funcionar más rápido así el servicio de encomiendas es más eficiente? |
|
| Algunos derechos reservados.
Se permite reproducir este material sin lastimarlo y citando la fuente. Última actualización dic-06. Buenos Aires, Argentina. |
|
|
|

