NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Leyes de Newton, cuerpos vinculados, plano inclinado, rozamiento)
|
|

|
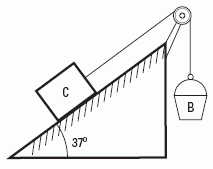
dN2.11- En un sistema como el que muestra la figura,
la caja C de 5 kg y el balde B de 2 kg están
y permanecen en reposo.
Se puede despreciar el rozamiento entre la
cuerda y la polea, y sus respectivas masas.
|
Determinar
la intensidad y sentido de la fuerza de
rozamiento entre la caja y el plano, en este caso.
Se va echando arena dentro del balde hasta totalizar
con el mismo un peso de 40 Newton. En
esas condiciones el sistema comienza a moverse,
y adquiere una aceleración de 0,4 m/s².
Calcular los coeficientes de rozamiento entre
la caja y el plano. |
 |
|
|
| Acá tenemos tres situaciones diferentes. Hasta que no las tengas a las tres suficientemente identificadas no sigas, ¿ok? La primera es una situación estática que, ya vas a ver... no es tan simple como parece. La segunda es una situación también estática, pero límite: el equilibrio está a punto de romperse. La tercera situación es dinámica. Son tres... si no te cierra estas afuera.
Te aclaro que este ejercicio es laaargo como esperanza de pobre. Arremangate.
Vamos a la primera situación y los DCL correspondientes. |
|
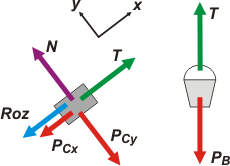 |
Este paso tiene dos dificultades. La primera es que no hay -a priori- forma de saber hacia dónde apunta la fuerza de rozamiento. Tal vez hacia abajo -como la representé-, tal vez hacia arriba -qui lo sá-. En estos casos lo más saludable es tirar una monedita y seguir adelante; el resultado (el signo del resultado) nos dirá si la monedita acertó o si la fuerza apuntaba en el sentido contrario al supuesto.
La segunda dificultad es más bien una trampa (un vicio) en la que caen decenas de miles de incautos estudiantes: donde ven una fuerza de rozamiento reemplazan por... |
|
|
Roze = μe . N
¡Nooo...! Sólo la fuerza de rozamiento estática máxima puede reemplazarse así.
Hechas todas las aclaraciones, vamos a resolver la primera parte del ejercicio. Este es el set de ecuaciones de Newton.
bloque C, eje x → T — PCx — Roze = 0 [1]
bloque C, eje y → N — PCy = 0 [2]
balde, eje x → PB — T = 0 [3]
La segunda ecuación no aporta nada interesante en esta etapa. Las otras dos tienen todo lo que hace falta. Las voy a sumar.
T — PCx — Roze + PB — T = 0
Roze = PB — PCx
Roze = PB — PC sen 37°
|
|
| |
Roze = — 10 N |
primera respuesta |
|
|
Eso me indica que apuntaba hacia el otro lado, o sea hacia arriba. Si no fuera por el rozamiento, el bloque empezaría a deslizar hacia abajo, ¿se entiende?
Bueno, ahora vamos a la segunda situación. Sigue siendo estática, pero ahora es la situación límite: el rozamiento estático ahora sí es el máximo... y ahora no hay duda que apunta hacia abajo. Para distinguir esta situación de la anterior, el nuevo peso del balde lo voy a llamar PBL (por balde lleno). Un granito más de arena que metas en el balde y se rompe el equilibrio... pero no lo metas, esperá un cacho que resolvemos esta parte del ejercicio.
bloque C, eje x → T — PCx — RozeM = 0 [4]
bloque C, eje y → N — PCy = 0 [5]
balde, eje x → PBL — T = 0 [6]
roz. est. máx. → RozeM = μe . NC [7]
Esta vez sí, van a tener que laburar las cuatro ecuaciones. Sumo la [4] con la [6],
RozeM = PBL — PCx
meto esto en la [7]
μe . N = PB — PCx
y reemplazo por la [5] (hay otro millón de caminos posibles)
μe = ( PBL — PCx ) / PCy
μe = ( PBL — PC sen 37°) / PC . cos 37°
|
|
| |
μe = 0,25 |
segunda respuesta |
|
|
Ahora sí: meté ese granito más de arena en el balde. Como estábamos en la situación límite, ese último granito rompe el equilibrio y el conjunto comienza a acelerar. El peso del balde no cambia (un granito no es nada).
bloque C, eje x → T — PCx — Rozd = mC . a [8]
bloque C, eje y → N — PCy = 0 [9]
balde, eje x → PBL — T = mBL . a [10]
roz. est. máx. → Rozd = μd . N [11]
Siguiendo el mismo camino algebraico de arriba llegás a la respuesta. Hacelo solo. |
|
| |
μd = 0,16 |
tercera respuesta |
|
|
| |
|
| |
| Si todavía te cuesta entender cómo se descompone la fuerza peso en un plano inclinado, te recomiendo leer este artículo. |
|
 |
| DESAFIO: ¿Cuánto debería valer la masa del balde para que, si el conjunto desliza lo haga a velocidad constante? Luego, si invirtiéramos el sentido de deslizamiento... ¿también lo haría a velocidad constante? |
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Última actualización jul-07. Buenos Aires, Argentina. |
|
|
|

