home  | más de dinámica | otros temas de Física | lecciones del maestro Ciruela | tonterías |  @ 
NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Leyes de Newton)

  

¡no me salen!

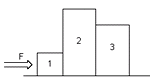
NMS 1.37 - En el sistema de la figura no hay rozamiento. Si las fuerzas C12 y C23 son las fuerzas de contacto entre los bloques, puede afirmarse que:

a) F = C12 = C23        b) F > C12 > C23         c) F < C12 < C23

d) F < C12 = C23        e) F > C12 = C23         f) nada
 

OK, este es un ejercicio requetefácil. Los profesores de Física suelen incluirlo (éste o una versión similar) en los exámenes con la pretensión de que los estudiantes los resuelvan pensándolo, razonándolo, apelando a la intuición o a algún razonamiento lateral. Quien puede hacer eso tarda no más de 3 minutos en arribar a la respuesta correcta. En cambio, resolverlo por la vía clásica es un poco más arduo.

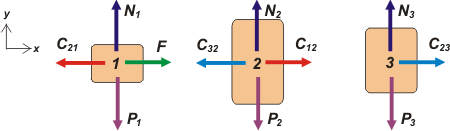
La vía clásica: empecemos con los DCLs.

    
 

Si tenés dudas de cómo hacer estos DCL te recomiendo que vayas al ejercicio
1.23

Está claro que C12 = C21 y que C23 = C32. Son los pares de interacción de las fuerzas de contacto entre los bloques.

Las ecuaciones verticales no las vamos a escribir... es obvio que en este ejercicio no aportan nada interesante.

    
bloque 1 →   ΣFx = m1 . a   →      F — C12 = m1 . a [1]
bloque 2 →   ΣFx = m2 . a →   C12 — C23 = m2 . a [2]
bloque 3 →   ΣFy = m3 . a →            C23 = m3 . a [3]
   

A la aceleración no le coloqué subíndice porque es la misma para los tres bloques. (A menos que los bloques sean deformables, todo lo que avance uno avanzará el otro en el mismo tiempo).

Con esas ecuaciones encontremos las expresiones par F, C12 y C23 y así las podremos comparar entre ellas. F es muy sencilla, basta con sumar miembro a miembro las 3 ecuaciones.

    

F — C12 + C12 — C23 +  C23 = m1 . a + m2 . a + m3 . a

    
          F = a . (m1 + m2 + m3)  
   

Ya tenemos un resultado para F que no depende de las otras fuerzas. Sigamos. Con ese resultado para F vamos a la ecuación [1] y lo reemplazamos:

a . (m1 + m2 + m3) — C12 = m1 . a

Y de ahí despejamos C12

C12 = — m1 . a + a . (m1 + m2 + m3)

    
          C12 = a . (m2 + m3)  
   
Y C23 ya lo tenemos solita en la ecuación [3]    
          C23 = a . (m3)  
   
Ahora compará los 3 resultados. Acordate que las masas son siempre números positivos (en lo que a nosotros respecta, no existen las masas negativas). Resulta obvia la respuesta:    
          F > C12 > C23 respuesta b)
   
Fijate que a este resultado llegamos sin interesarnos cuánto vale cada masa. Sean cuales sean sus valores la suma de las tres siempre será mayor que la suma de dos... etcétera.    

DISCUSION: La resolución clásica tampoco fue tan grave... no podés protestar. Pero para aquel estudiante que ejercitó su intuición dinámica (o sea, que no se conforma con arribar a resultados sino que los discute y se preocupa de entender cómo funcionan los sistemas) puede resultarle obvio que la fuerza F debe acelerar a tres bloques, la fuerza C12 debe acelerar a dos, y la fuerza C23 apenas debe acelerar un bloque solo.

Otro modo de verlo: suponete que sos una hormiga y quedás atrapado entre dos bloques... ¿entre cuáles dos preferirías haber quedado? Para responderte esta pregunta, tal vez te ayude a pensar que no son sólo 3 bloques... digamos 300. Tal como enseñaba Carroll: las cosas son más claras cuando exageramos.

    
DESAFIO: ¿Cuánto debería valer la masa 2 para que C12 y C23 sean iguales?  
Algunos derechos reservados. Se permite su reproducción bajo la solemne promesa de citar la fuente. Última actualización may-10. Buenos Aires, Argentina.