NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Leyes de Newton)
|
|

|
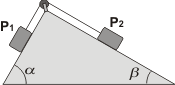
NMS 1.34 - En el sistema de la figura se conocen las masas de los cuerpos y los ángulos de inclinación de cada plano. Y se desea conocer la aceleración. Hallarla en función de las masas y los ángulos. |
 |
| |
|
| |
Ejercicio sencillo si los hay. Vamos con los DCL. |
|
|
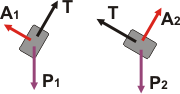 |
Sobre cada cuerpo actúan tres fuerzas: su propio peso, el apoyo con el plano y la fuerza que hace la soga. Llamé P1y P2 a los pesos.
Llamé A1y A2 respectivamente a los apoyos con el plano; y llamé T a las tensiones que como se corresponden con los extremos de la misma soga son iguales y no requieren subíndice. |
|
|
|
Con esos DCL no puedo operar, porque las fuerzas no son codireccionales. Voy a rehacer el DCL pero descomponiendo los pesos en las direcciones paralela y normal a los respectivos planos. |
|
|
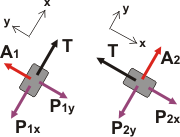 |
Ahora sí, de cada cuerpo escribiremos dos ecuaciones de Newton, una para x y otra para y.
En los ejes y, transversales al movimiento, no cabe duda: los cuerpos no se despegan de los planos inclinados. En el eje del movimiento, x, la aceleración vale 0 porque lo dice el enunciado (se desplazan a velocidad constante). |
|
|
|
| |
Cuerpo 1, eje x |
T — P1X = m1 . a |
[1] |
| |
Cuerpo 1, eje y |
A1 — P1y = 0 |
[2] |
| |
Cuerpo 2, eje x |
P2X — T = m2 . a |
[3] |
| |
Cuerpo 2, eje y |
A2 — P2y = 0 |
[4] |
|
|
| las aceleraciones de ambos cuerpos son iguales porque la cuerda se supone inextensible |
|
En este ejercicio las ecuaciones [2] y [4] no aportan nada, podemos olvidarlas. pero las ecuaciones [1] y [3] nos van a ser muy útiles. Sumémoslas miembro a miembro:
T — P1X + P2X — T = m1 . a + m2 . a
— P1X + P2X = (m1 + m2) . a
Ya vamos llegando. Tenemos que expresar esas componentes paralelas al plano en función de las masas y los ángulos respectivos. |
|
|
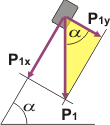
Si sos de los que todavía mete la pata cuando tiene que descomponer o recomponer una fuerza (o un vector cualquiera), ponete las pilas, sería una pena que por ese motivo no llegues al resultado correcto. Te doy una ayuda correspondiente al cuerpo 1.
El ángulo α (la inclinación del cuerpo 1) vuelve a aparecer a la derecha de P1, por lo tanto, si mirás el triangulito rectángulo que te sombré en amarillo... resulta que:
P1X = P1 sen α = m1 g sen α
|
|
|
|
|
Y si trabajás análogamente con el cuerpo 2, sin confundirte, encontrás que:
P2X = P2 sen β = m2 g sen β
Entonces sí... volvamos a la ecuación que había quedado pendiente y reemplacemos con lo que acabamos de averiguar.
— m1 g sen α + m2 g sen β = (m1 + m2) . a
(— m1 sen α + m2 sen β) g = (m1 + m2) . a
Listo. Despejemos a. |
|
|
| |
a = g (— m1 sen α + m2 sen β) / (m1 + m2) |
|
|
|
|
| Con ese resultado podés jugar bastante. Fijate qué pasa a) si la aceleración vale cero; b) si α vale 90º y β 0º; c) si m1 valiese 0. Etcétera. Deberás encontrar resultados de ejercicios que ya hiciste. |
|
|
Tenés este mismo ejercicio con una dificultad más acá.
|
|
|
| DESAFIO: ¿Escribir la condición para que la aceleración tenga sentido contrario al sentido de las equis? |
|
 |
| Algunos derechos reservados.
Se permite su reproducción bajo la solemne promesa de citar la fuente. Última actualización oct-11. Buenos Aires, Argentina. |
|
|
| |
|

