home  | más de dinámica | otros temas de Física | lecciones del maestro Ciruela | tonterías |  @ 
NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Leyes de Newton)

  

¡no me salen!

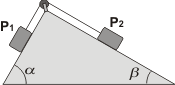
NMS 1.47* - En el sistema de la figura se desplaza a velocidad constante y con rozamiento despreciable hacia la derecha (α = 60º, β = 30º). Entonces:
 

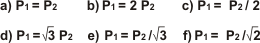Ejercicio sencillo si los hay. Aunque no lo creas, una de las principales dificultades que encontraron los estudiantes para resolver el ejercicio es que no entendían el significado de las posibles respuestas, me refiero a las respuestas d), e) y f).

Lamentablemente, la única solución para esa dificultad es ganar experiencia, tener horas de vuelo, haber hecho cientos de ejercicios, dejar de ser creyente.

Raíz de 3, (3½, otra forma más de escribirlo) es lo mismo que 1,732... cualquier calculadora lo sabe. Al final del ejercicio te cuento por qué el autor del ejercicio puso raíz de 3 en lugar de 1,732...

También he visto muchos estudiantes que frente a un ejercicio como éste se quedan inmóvilen contemplando la grilla de respuestas como si fruto de esa contemplación pudiera salir el resultado... ¡no pierdas tiempo, ponete a resolverlo!

Vamos con los DCL.

    
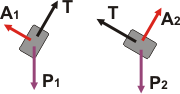Sobre cada cuerpo actúan tres fuerzas: su propio peso, el apoyo con el plano y la fuerza que hace la soga. Llamé P1y P2 a los pesos, que no son otra cosa que las incógnitas que figuran en las respuestas posibles, o sea, tenemos que decidir qué relación hay entre ambos (¿será uno el doble que el otro?, ¿será 1,732 veces más grande uno que otro?...);
   

Llamé A1y A2 respectivamente a los apoyos con el plano; y llamé T a las tensiones que como se corresponden con los extremos de la misma soga son iguales y no requieren subíndice.

Con esos DCL no puedo operar, porque las fuerzas no son codireccionales. Voy a rehacer el DCL pero descomponiendo los pesos en las direcciones paralela y normal al plano.

    

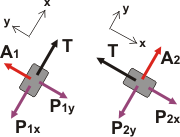Ahora sí, de cada cuerpo escribiremos dos ecuaciones de Newton, una para x y otra para y.

Las cuatro ecuaciones irán igualadas a 0. En los ejes y, transversales al movimiento, no cabe duda: los cuerpos no se despegan de los planos inclinados. En el eje del movimiento, x, la aceleración vale 0 porque lo dice el enunciado (se desplazan a velocidad constante).
   
  Cuerpo 1, eje x           T — P1X = 0 [1]
  Cuerpo 1, eje y           A1 — P1y = 0 [2]
  Cuerpo 2, eje x           P2X — T = 0 [3]
  Cuerpo 2, eje y           A2 — P2y = 0 [4]
   

En este ejercicio las ecuaciones [2] y [4] no aportan nada, podemos olvidarlas. pero las ecuaciones [1] y [3] nos van a ser muy útiles. Sumémoslas miembro a miembro:

T — P1X + P2X — T = 0

          — P1X + P2X = 0

                   — P1X = — P2X

                       P1X = P2X

Ya vamos llegando. Todavía no tenemos una relación entre los pesos, pero ya tenemos una relación entre las componentes x de los pesos.

   

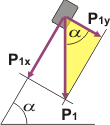
Si sos de los que todavía mete la pata cuando tiene que descomponer o recomponer una fuerza (o un vector cualquiera), ponete las pilas, sería una pena que por ese motivo no llegues al resultado correcto. Te doy una ayuda correspondiente al cuerpo 1.

El ángulo α (la inclinación del cuerpo 1) vuelve a aparecer a la derecha de P1, por lo tanto, si mirás el triangulito rectángulo que te sombré en amarillo... resulta que:

P1X = P1 sen α

   

Y si trabajás análogamente con el cuerpo 2, sin confundirte, encontrás que:

P2X = P2 sen β

Ahora podés meter esta información en la última igualdad que dejamos esperando,

P1 sen α = P2 sen β

P1= P2 sen 30º / sen 60º

    
         P1= P2 0,577... respuesta e)
   
Porque 1 dividido raíz de 3 (que es lo que figura en la opción e) como factor de P2) es 0,577...    
     

DISCUSION: Cuando tengas más experiencia no vas a necesitar hacer todo el planteo del ejercicio, paso por paso, como te lo hice yo acá. Con un vistazo vas a comprender que la componente "libre" del peso del cuerpo 1 tira para su lado (la izquierda) tanto como la componente "libre" del peso del cuerpo 2 tira para el suyo (derecha). O sea:

P1 sen α = P2 sen β

Habrás visto que todos los resultados numéricos que te puse tienen puntos suspensivos. El motivo es que el sen 60º, por ejemplo, es un número irracional, de infinitas cifras decimales. Pero se puede expresar de manera exacta así: 3½/2, que, entre paréntesis, es igual a sen 60º.

    
*Este ejercicio pertenecía al tema de examen parcial de Física tomado el 9 de mayo de 2005 en diversas sedes del CBC.
   
DESAFIO: ¿Si en lugar de moverse a la derecha el conjunto se estuviera moviendo hacia la izquierda, ¿cuál sería la relación entre los pesos?  
Algunos derechos reservados. Se permite su reproducción bajo la solemne promesa de citar la fuente. Última actualización sep-10. Buenos Aires, Argentina.