NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(rozamiento y elásticas)
|
|

|
| |
|
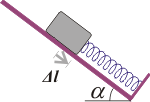
FIS 88 (d5.10) - Un bloque de masa m se coloca sobre un plano inclinado unido
a un resorte de largo natural lo y constante elástica k. El plano
inclinado forma un ángulo α con la horizontal.
Datos: lo = 60 cm, k = 500 N/m, m = 30 kg y α = 37º.
a) Suponiendo que el plano está perfectamente pulido, calcular la
posición de equilibrio del bloque con respecto al extremo fijo del
resorte.
|
 |
b) Si los coeficientes de rozamiento estático y dinámico entre el
bloque y el plano fueran μe = 0,4; μd = 0,15, respectivamente, hallar la
máxima longitud que podrá darse al resorte sin romper el equilibrio.
c) Con los mismos coeficientes anteriores, hallar la mínima longitud del resorte que conserve el
equilibrio. |
|
|
¡Problema tramposo si los hay! Pero no te llenes de rebeldía tonta, bienvenida sea la trampa si le extraemos una enseñanza duradera. Las trampas cuestionables son las de los exámenes... ¡y solo eso: cuestionables! ¡Te espero en la esquina!
¡Ah...! Arrugaste... Bueno... vamos a ver si entendemos en qué consiste la trampa y cómo haríamos para no caer en ella el fatídico día del examen. Esta trampa más típica que el verdulero se llama los datos que sobran. La usamos 9 de cada 10 veces, y nos reporta un placer enorme ver cómo caen los pajaritos. Los pajaritos que no saben física, y que son aplicadores de fórmulas al tun-tún, y que tratan de llenarlas (para eso las tienen en el machete) con los datos disponibles. Vos no hagas eso... ¡never! Vos que sos un pollo de No me salen, vas a usar el DCL para pensar el problema, para discutirlo, para contrastarlo con tu intuición, para contrastarlo con cada cosa que dice el enunciado... Vos, pollito, pollita, no vas a caer en la trampa. (Viste, ya nos amigamos).
Vamos entonces a los DCLs, tenemos tres situaciones diferentes, hagamos uno para cada una de ellas. En ellas voy a llamar Δxi al estiramiento del resorte en la primera instancia, cuando no hay rozamiento, ΔxM y Δxm al estiramiento máximo y al mínimo respectivamente. |
|
|
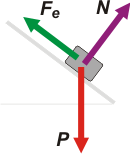 |
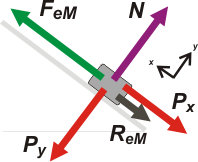
Acá tenés la situación inicial, bastante sencilla, hay tres fuerzas actuando sobre la caja. La fuerza elástica, Fe, que es paralela al plano inclinado. La fuerza de apoyo, N, que es perpendicular (o normal, para que te quedes contento) al plano, y la fuerza peso, P, que es vertical. Voy a descomponer a la última en dos direcciones: una dirección normal y otra perpendicular al plano.
Acordate que ahora estamos sin rozamiento. |
|
|
|
| Ahí te coloqué el SR, para que no te pierdas. |
|
|
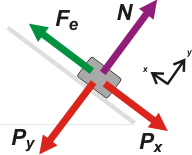 |
Sigue siendo la situación inicial, en que no hay fuerza de rozamiento y la caja está en equilibrio. Fijate (y controlá) que
Px = P sen α
Py = P cos α
y acordate que Fe = k Δxi |
|
|
|
Como ΣFx = 0 y ΣFy = 0, ya que el cuerpo esta en equilibrio no cabe otra que
P sen α = k Δxi
N = P cos α (esta no aporta nada interesante por ahora)
Δxi = P sen α / k
Δxi = 300 N . 0,6 / 500 N/m
Δxi = 0,36 m
No te olvides de que esta deformación es una compresión, el cuerpo está comprimiendo al resorte.
Li = L0 − Δxi
Li = 0,60 m − 0,36 m
|
|
|
|
|
|
Vamos a la segunda pregunta, nos piden hallar la máxima longitud que
podrá darse al resorte sin romper el equilibrio. Habiendo rozamiento no es que el resorte se vaya a estirar solo... tenés que tomar el cuerpo con la mano, correrlo hacia arriba y suavemente, deslizarlo hacia abajo hasta que se queda en equilibrio. Vas a notar que la compresión del resorte es diferente a la anterior, menor... el motivo es que está actuando la fuerza de rozamiento.
Si imaginás una máxima longitud imaginarás un resorte que se comprime menos de lo que estaba antes... o sea la fuerza elástica debe ser menor en este caso que en el anterior. No puede ser que Px haya disminuido, pues P es constante, la unica posibilidad (bastante inducida por el resto de la información) es que aparece una fuerza de rozamiento que "traba" antes de que descienda hasta la compresión anterior. |
|
|
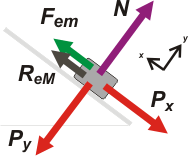 |
Nuevamente ΣFx = 0 y ΣFy = 0, ya que el cuerpo sigue en equilibrio y ahora FeM = k . ΔxM. Por otro lado el rozamiento debe ser estático... pero además debe ser el estático máximo, para corresponderse con la mínima compresión del resorte (un milímetro más y se rompe el equilibrio). Y no te olvides que
ReM = μe . N
Bueno, con toda esta elucubración, reescribamos las ecuaciones de x e y |
|
|
|
Fem + ReM = P sen α → k ΔxM = P sen α − μe . N
N = P cos α (ahora sí aporta, pues la reemplazo arriba)
k ΔxM = P sen α − μe . P . cos α
ΔxM = (P sen α − μe . P . cos α) / k
ΔxM = (300 N . 0,6 − 0,4 . 300 N . 0,8) / 500 N/m
ΔxM = 0,168 m
LMáx = L0 − ΔxM
LMáx= 0,60 m − 0,168 m
|
|
|
| |
LMáx= 0,432 m |
respuesta b) |
|
|
|
| Y ahora abordemos la última pregunta, que pide hallar
la mínima longitud del resorte que conserve
el equilibrio. Pide lo mismo que antes pero al revés... mínima longitud... máxima fuerza... equilibrio. Acá es donde todos los pajaritos meten la pata en la trampa... pero vos no. |
|
|
 |
¿Cazaste? Los pajaritos ponen una fuerza de rozamiento dinámica... qué tiene que ver... invento puro... "para algo me habrán dado el coeficiente dinámico... qué se yo"...
Seamos serios. De nuevo ΣFx = 0 y
ΣFy = 0, ya que el cuerpo sigue en equilibrio y ahora Fem = k Δxm.
Y el rozamiento nuevamente debe ser
ReM = μe . N, si no, ese no sería el estiramiento mínimo. |
|
|
|
Fem = P sen α + ReM → k Δxm = P sen α + μe . N
N = P cos α (igual que antes)
k Δxm + μe . P cos v = P sen α
Δxm = (P sen α + μe . P . cos α) / k
Δxm = (300 N . 0,6 + 0,4 . 300 N . 0,8) / 500 N/m
Δxm = 0,552 m
Lmín = L0 + Δxm
Lmín= 0,60 m − 0,552 m
|
|
|
| |
Lmín= 0,048 m |
respuesta c) |
|
|
|
| |
|
|
La vision macroscópica. A muchos estudiantes les cuesta entender la dinámica de este ejercicio porque chocan con la mayor dificultad de las fuerzas de rozamiento: les cuesta predecir hacia dónde apuntan. Pues no deben desmoralizarse: a la humanidad le costó 2000 años descubrirlas y entenderlas, no hay que pretender encontrarles la vuelta en un curso de Física de apenas 4 meses. El gran problema de las fuerzas de rozamiento es que actúan a escondidas y obedecen a razones microscópicas.
Te ofrezco esté método que yo desarrollé y permite razonar un fenómeno de escala microscópica imaginándolo como actuando de modo macroscópico. Se trata del diente delator. Podés verlo acá. Pero ahora quedate y seguí con éste. |
|
 |
 |
|
Imaginá todas las rugosidades de las superficies en contacto, todas pequeñitas o microscópicas reunidas ahora en una única y grande mordedura: el plano tiene una única rugosidad, grandota, que se mete en una única arruga del bloque, también grandota.
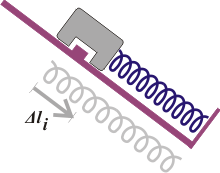
En la primera etapa de este ejercicio el rozamiento no actúa. El resorte está estirado pero sólo para sostener la parte del peso que no se banca el plano. El rozamiento no afecta: no hay contacto lateral entre el plano y el cuerpo. |
| Primera parte del ejercicio: no hay rozamiento o, si lo hay, no actúa. El cuerpo está en equilibrio. |
|
|
 |
|
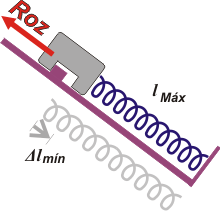
Levantá un poco el cuerpo y apoyalo más arriba. El cuerpo no desciende hata la posición anterior... rozamiento lo traba. Fijate cómo lo aclara el dibujo. El diente delator (que resume todas las interacciones microscópicas del rozamiento debidas a las irregularidades de las superficies) muestra claramente que el plano hace una fuerza hacia arriba (paralela al plano) sobre el cuerpo.
Si lo corrieras hacia arriba un poquito más, las rugosidades no aguantarían más, soltarían el cuerpo y se rompería el equilibrio. Sin duda, la situación que describíamos era la estática máxima. |
| Segunda parte del ejercicio: el resorte se estira al máximo posible sin que el cuerpo deslice. |
|
|
 |
|
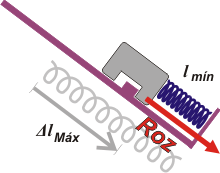
La última parte es la que más cuesta. Prestá atención. Si empujás el cuerpo hacia abajo y acortando la longitud del resorte... seguramente deberás volver a pasar por la situación inicial. Pero no te detengas... seguí comprimiendo el resorte. Al acortarse la fuerza elástica es mayor... Hay un lugar preciso en que el cuerpo no rebota, hay que saber buscarlo. No cabe duda que las superficies están trabadas (por rozamiento) pero para el lado contrario que el anterior.
|
| Tercera parte del ejercicio: el resorte se encoge lo más posible sin que el cuerpo deslice. |
|
|
Si seguís comprimiendo llegará el momento en que el rozamiento no puede sostener más al cuerpo... pero no llegues a ese extremo, repetí el experimento y detenelo un milímetro antes de que el deslizamiento se produzca. En esa situación el rozamiento será el estático máximo... pero apuntando hacia abajo.
En los tres casos el resorte está comprimido (más corto que como viene de fábrica, que está representado en gris) siempre hace fuerza hacia arriba. La prueba de ello son los resultados obtenidos: siempre compresiones, nunca estiramientos. Eso no quita que podría funcionar al revés: si el coeficiente de rozamiento fuese muy grande bien podríamos encontrar un equilibrio del estilo de la tercera parte de este ejercicio pero con el resorte comprimido... pero, aunque nada lo impide, no es el caso. |
|
| DESAFIO: Inventá una situación lo más parecida a esta posible... pero usando el coeficiente de rozamiento dinámico. (Si no lo sacás no existís). |
|
| Algunos derechos reservados.
Se permite tu reproducción pero ahí no me cites. Última actualización jun-16. Buenos Aires, Argentina, América Latina, Planeta Tierra, Sistema Solar, Galaxia Via Láctea, Universo. |
|
|
|

