 |
NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Fuerzas elásticas)
|
|

|
| |
 |
FIS 83 (d5.04) - Un hombre está de pie sobre una balanza
de resorte. De repente se pone en cuclillas. ¿Qué ocurre con la lectura de la balanza?¿Y si el
hombre estuviera inicialmente en cuclillas y se
levantara repentinamente? |
|
Este ejercicio es fundamental. Es una suerte que estés acá. Los profesores suelen pasarlo por alto (yo me incluyo). Pero es importantísimo. Ojalá lo aproveches.
|
 |
Lo primero que tenemos que hacer es comprender esa situación simple que significa subirse a una balanza y pesarse... te apuesto que si terminás comprendiéndola y te dedicás a investigar qué cree la gente común (o un estudiante de Física) sobre el asunto, vas a encontrar que nadie entiende una jota.
Ahí tenés un tío subido a la balanza en la farmacia de la esquina. Que la balanza funcione con resortes no agrega ni quita nada en este ejercicio, la importancia de esa característica se discute en el problema adicional 17.
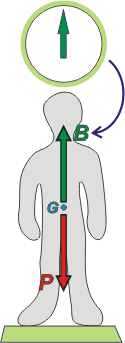
Vamos a suponer, por comodidad, que las fuerzas que sobre él actúan lo hacen en su centro de masa -que en este ejercicio va a tener un rol protagónico- que te indiqué con un punto celeste, G, cercano al ombligo del chabón.
Las fuerzas que actúan sobre el hombre en esa situación son: la atracción gravitatoria de la Tierra, P, vulgarmente llamada peso. Y la fuerza con que la balanza lo sostiene, lo ataja, lo empuja hacia arriba, B, y que en cualquier clase de física y cualquier libro de texto la llamarían normal.
La balanza lee esa fuerza, B. No lee el peso del hombre. El display de la balanza indica el valor de la fuerza que hace la propia balanza, hacia arriba, con la pequeña plataforma a la que vos te subís. |
|
|
|
Habrás notado que cuando te subís a la balanza la aguja del display oscila un rato hasta que se estabiliza sobre un numerito. Ese numerito es el que te interesa, porque es el que indica también tu peso (una medida de todo lo que comiste los últimos meses, los rollitos... etc.). También aprendiste que para obtener rápidamente ese numerito tenés que subirte y tratar de no moverte lo antes posible. Lógico: porque la clave es que tu aceleración sea cero. Sólo en ese caso: que no te muevas y tu aceleración valga cero, tu peso va a ser igual a la fuerza que hace la balanza y el display va a indicar el numerito que te interesa. Lo afirma la ley de Newton, mirá:
B — P = m . a
Si te quedás quieto, tu aceleración valdrá cero...
B — P = 0
B = P
Recién ahí la indicación de la balanza te revela lo que pesás.
Ahora vamos a ver qué pasa si el ñato decide ponerse en cuclillas. |
|
|
|
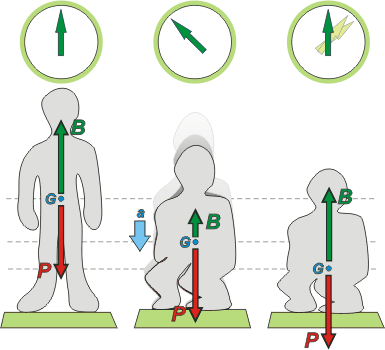
La situación que nos interesa es la representada en el medio, o sea, mientras, el hombre se pone en cuclillas.
Al final termina agachado... pero en reposo. A los fines de la dinámica es lo mismo que esté parado o arrodillado: mientras su aceleración valga cero, la lectura de la balanza será igual al peso.
Pero mientras... la aceleración del centro de masa puede ser distinta de cero (no todas las personas se agachan de la misma manera... y también es posible hacerlo sin aceleración alguna, pero lo más común es hacerlo de esta manera). |
|
De modo que lo más probable es que haya una aceleración del centro de masa que apunte hacia abajo, y la ecuación de Newton pasará a decir...
B — P = m . a
De modo que la resultante de las dos fuerzas tenga el mismo sentido que la aceleración... o sea... hacia abajo. La fuerza peso es constante (al menos durante una visita a la farmacia), de modo que la que está variando debe ser la fuerza en la plataforma de la balanza, o sea B. Mientras el hombre se esta agachando la indicación de la balanza será menor que su peso.
Es probable que en el breve lapso en que termina el movimiento -muy cercano a la última imagen del esquema- el sentido de la aceleración se invierta (ya que nuestra capacidad de plegarnos es finita, y el ombligo suele frenarse con cierta brusquedad). De modo que es probable que en ese breve lapso la indicación de la balanza pegue un salto hacia valores mayores que nuestro peso.
Ahora veamos qué pasa cuando el hombre vuelve a pararse. |
|
|
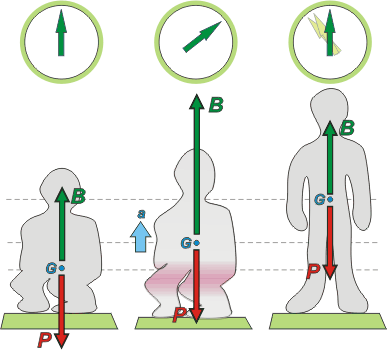 |
Acá, nuevamente, lo que interesa es el durante el estiramiento para volver a estar parado. Lo más probable -no hay una única forma de hacerlo- es que se realice de esta manera: haciendo fuerza con nuestros muslos (fijate que los puse un poco enrojecidos) hacemos una fuerza superior sobre la plataforma de la balanza.
Ella nos responde vengativamente (no es que sea mala sino que obedece el Principio de la Acción y Reacción) y realiza sobre el hombre una fuerza de contacto, B, mayor que antes, y la lectura de la balanza lo refleja.
Fijate que siempre dibujé la fuerza peso del mismo largo. |
|
La descripción según Newton sería ésta: mientras el tipo se levanta acelerando su centro de masa, la aceleración es distinta de cero y tiene el mismo sentido de la fuerza con que nos sostiene la balanza. La Segunda Ley dice:
B — P = m . a
Momentáneamente esa fuerza se hace mayor que el peso... y así lo indica la balanza.
Acá también conviene aclarar que cuando el hombre alcanza su elongación máxima (última figura del esquema) su centro de masa -que se venía moviendo hacia arriba- debe detenerse y es probable que se haga necesaria una aceleración hacia abajo. Por eso es probable que en ese breve lapso en que nos terminamos de estirar, la balanza indique brevemente valores oscilantes menores que el peso... no hay que ilusionarse. |
|
|
DISCUSION: Fue largo pero creo que valió la pena. Creeme, aunque la situación narrada en el enunciado es recontra sencilla... tuve que resumirla enormemente, una descripción acabada del proceso podría llevarnos varias carilla más.
|
|
 |
DESAFIO: Hacer un gráfico de aceleración/tiempo, en tándem con otro de fuerza/tiempo, que describa todo el proceso desde que el hombre se sube en la balanza hasta que se baja, con una encuclillada en el medio. En el gráfico de aceleración debe describir la del centro de masa, y el de fuerza/tiempo indicar la fuerza peso y la fuerza con que sostiene la balanza. Si se lo mostrás a tu profesor para que te lo corrija, a la fuerza de la balanza la tenés que llamar normal (evitemos males mayores). |
|
| Algunos reservados (no es que sean tímidos, callados).
Se permite su reproducción citando la fuente; se puede prestar y/o regalar, se prescriben abrazos como recompensa. Última actualización jun-08. Buenos Aires, Argentina. |
|
|
|

