 |
NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Leyes de Newton, dinámica del movimiento circular)
|
|

|
| |
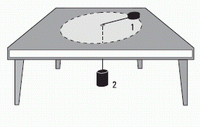
FIS 65 (d3.18) - Un cuerpo de masa m se encuentra apoyado sobre una mesa
horizontal sin rozamiento. El cuerpo está unido a un bloque de masa M2 colgado mediante una cuerda ideal que pasa por un agujero practicado
en la mesa. El cuerpo de masa M2 está en reposo, mientras que el de
masa m1 describe un movimiento circular uniforme de radio r.
|
a) Realizar los diagramas de cuerpo libre. Especificar los pares de
acción-reacción.
b) Calcular el módulo de la velocidad con la que gira el cuerpo que se encuentra sobre la mesa.
¿Cuánto valen la intensidad de la aceleración tangencial y la de la aceleración centrípeta?
Datos: m1 = 1 kg, M2 = 4 kg, r = 0,1 m |
 |
|
| El ejercicio éste es más fácil de lo que el común de los mortales anticipa. Lo principal es que te des cuenta de que la soga que une los cuerpitos es una soga ideal, de CBC, sin masa, inextensible, inoxidable, etcétera. De modo que la fuerza que ejerce sobre una masa es la misma que la que ejerce sobre la otra masa. |
|
|
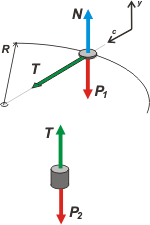 |
En el caso de la de abajo, es fácil ver que la tensión, T, es igual al peso. Y que deben ser iguales dado que ese cuerpo no sube ni baja. Eso lo sabemos porque el radio de giro de la de arriba (el tramo de soga sobre la mesa) es constante.
De modo que (para el cuerpo 2):
Σ Fy = 0
T — P2 = 0
T = M2 . g
|
|
|
|
De ahí sale inmediatamente la tensión de la cuerda:
T = 4 kg . 10 m/s²
T = 40 N
Para el cuerpo 1, la tensión es la fuerza centrípeta que lo hace girar. Las otras dos -su peso y el apoyo en la mesa- son verticales y se cancelan entre sí. Eso lo sabemos porque el cuerpo 1 no levanta vuelo ni se hunde en la mesa.
T = m1 . ac1
T = m1 . v1² / R
De ahí despejamos la velocidad y la calculamos:
v1² = T . R / m1
v1² = 40 N . 0,1 m / 1 kg
|
|
|
|
|
|
En cuanto a las aceleraciones, ya lo dijimos...
ac1 = v1² / R
|
|
|
|
|
|
| |
|
|
DISCUSION: Pareciera que toda la dificultad de este ejercicio consistía en admitir que el cuerpo de abajo de la mesa no necesariamente debía estar cayendo: podía estar quieto... o también, subiendo. Todo depende de un entretenido jueguito dinámico.
NOTA: tenés este mismo ejercicio con otras variantes acá. |
|
 |
| DESAFIO: ¿Qué ocurriría si la mesa tuviese rozamiento? |
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente... ¡Ojímetro! Última actualización abr-16. Buenos Aires, Argentina. |
|
|
|

