 |
NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Leyes de Newton, dinámica del movimiento circular)
|
|

|
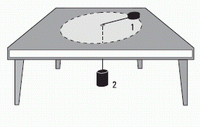
| NMS d3.07- El cuerpo 1 gira sobre una mesa horizontal
con rozamiento despreciable, mantenido por
una cuerda que pasa por un orificio en su centro,
de la que cuelga el cuerpo 2. |
a- Si ambos cuerpos tienen masas iguales, hallar
la frecuencia con que el cuerpo 1 describe
una circunferencia de 0,4 m de radio.
b- Hallar el nuevo radio para duplicar la frecuencia
anterior sin cambiar los cuerpos.
c- Hallar la relación de masas entre el cuerpo 2
y el 1, para que éste gire con la frecuencia calculada
en el inciso a y con el radio del inciso b. |
 |
|
| El ejercicio éste es más fácil de lo que el común de los mortales anticipa. Lo principal es que te des cuenta de que la soga que une los cuerpitos es una soga ideal, de CBC, sin masa, inextensible, inoxidable, etcétera. De modo que la fuerza que ejerce sobre una masa es la misma que la que ejerce sobre la otra masa. |
|
|
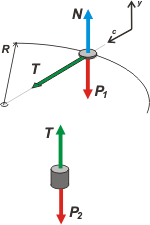 |
En el caso de la de abajo, es fácil ver que la tensión, T, es igual al peso. Y que deben ser iguales dado que ese cuerpo no sube ni baja. Eso lo sabemos porque el radio de giro de la de arriba (el tramo de soga sobre la mesa) es constante.
De modo que (para el cuerpo 2):
ΣFy = 0
T — P2 = 0
T = m2 . g
|
|
|
|
Para el cuerpo 1, la tensión es la fuerza centrípeta que lo hace girar. Las otras dos -su peso y el apoyo en la mesa- son verticales y se cancelan entre sí. Eso lo sabemos porque el cuerpo 1 no levanta vuelo ni se hunde en la mesa.
T = m1 . ac
Si unimos ambas ecuaciones, nos queda:
m2 . g = m1 . ac
m2 . g = m1 . ωa² . Ra
m2 . g = m1 . 4π² . ƒa² . Ra [1]
Guardo esta expresión en mi corazón porque sé que me va a servir después, y despejo la frecuencia recordando que las masas son iguales.
ƒa² = g / 4π² . Ra
|
|
|
|
|
|
Para resolver la segunda cuestión me basta con arrancar de [1], porque estamos en la misma sólo que con otros datos.
m2 . g = m1 . 4π² . ƒb² . Rb
Rb = g / 4π² . ƒb²
|
|
|
|
|
|
Para la tercera, lo mismo... arranco otra vez de [1] (ya me aburrí).
m2 . g = m1 . 4π² . ƒa² . Rb
m2 / m1 = 4π² . ƒa² . Rb / g
|
|
|
|
|
|
| |
|
|
DISCUSION: Pareciera que toda la dificultad de este ejercicio consistía en admitir que el cuerpo de abajo de la mesa no necesariamente debía estar cayendo: podía estar quieto... o también, subiendo. Todo depende de un entretenido jueguito dinámico.
|
|
 |
| DESAFIO: Tomá el canuto vacío de una birome gastada. Enhebrale un piolín de más o menos un metro y medio. Atá en ambos extremos del piolín masa de alrededor de 100 gramos cada una, no tienen por qué ser iguales. Andá a un espacio abierto como un jardín, o una vereda. Jugá. |
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente... ¡Ojímetro! Última actualización jul-08. Buenos Aires, Argentina. |
|
|
|

