home  | más de dinámica | otros temas de Física | lecciones del maestro Ciruela | tonterías |  @ 
  NO ME SALEN
   PROBLEMAS RESUELTOS DE FÍSICA DEL CBC

  

¡no me salen!

 
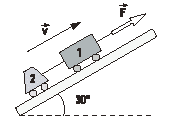
FIS d1.16- El sistema de la figura asciende por el plano inclinado 30°, que presenta rozamiento despreciable. Las masas de los cuerpos son m1= 60 kg, m2= 40 kg. Hacer los diagramas de cuerpo libre en cada caso, y determinar:
    a- La intensidad de la fuerza F necesaria, para que se mueva con velocidad constante.
    b- La fuerza que ejerce la cuerda, en ese caso.
   c- La intensidad de F necesaria para que se aceleren hacia arriba a razón de 2 m/s², y la fuerza que soporta la cuerda en ese caso.
    d- La fuerza que soporta la cuerda, la aceleración y el sentido del movimiento, un instante después de suprimir F.
 
Sin dudarlo un instante... ¡marchen dos DCL!    
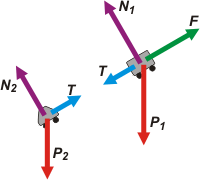Sobre cada carrito actúa la Tierra atrayendo a ambos con fuerza P1 y P2. El plano inclinado les da apoyo a ambos, en ambos casos con fuerzas perpendiculares (normales) al plano, y con fuerza N1 y N2. Sobre cada carrito, también, actúa una soga que al no tener masa apreciable realiza la misma fuerza en ambos extremos, o sea, sobre cada carrito, T. Y sólo sobre el carrito 1 actúa esa fuerza exterior que no sabemos quién la ejerce pero no importa, se trata de un dato del enunciado, F.
   
¡Marche un SR y una descomposición vectorial!    
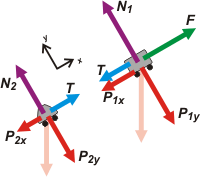diagrama de cuerpo libre - No me salen

Como las fuerzas presentes apuntan en direcciones diversas, elegimos un SR adecuado y las fuerzas que no coinciden con esas direcciones las descomponemos, y las reemplazamos.

Le tocó a las fuerzas peso, ser reemplazadas por sus componentes paralelas y perpendiculares al plano.

   
Naturalmente, se vienen las ecuaciones de Newton.    
Cuerpo 1 → ΣFx = m1 ax →

F — P1X — T

= 0
→ ΣFy = m1 ay → N1 — P1y = 0
Cuerpo 2 → ΣFx = m2 ax →  T — P2X = 0
→ ΣFy = m2 ay → N2 — P2y = 0
   

Nuevamente, las ecuaciones en y no aportan información relevante para este problema, pero las de x sí. Tené en cuenta que:

P1X = P1 sen α = m1 g sen α

P2X = P2 sen α = m2 g sen α

Vamos al álgebra... de la ecuación de x del cuerpo 2 despejo T...

T = m2 g sen α

  
Si te cuesta entender el asunto de la descomposi-ción de la fuerza peso, te recomiendo leer este apunte.
  T = 200 N la pregunta b)
   

eso lo meto en la ecuación de x del cuerpo 1 y despejo F:

F = m1 g sen α + m2 g sen α

    
  F = g sen α (m1 + m2)  
   
F = 10 m/s² . 0,5 . 100 kg
    
  F = 500 N la pregunta a)
   
No pretendas que siga yo... en las ecuaciones de x de los dos cuerpos, en lugar de igualar a cero, igualá a 2 m/s² y volvé a calcular. Y en cuanto a la última pregunta podés razonarla sin ayuda, simplemente tené en consideración que la aceleración de ambos cuerpos debe ser la de cualquier otro sobre un plano inclinado sin rozamiento ni fuerzas exteriores aplicadas sobre él. O sea, lo que viste en el problema del esquiador, el 1.10.   ¿Tenés ganas de leer algo que te vuele la cabeza?
     
DISCUSION: Fijate la ecuación que marqué en amarillo. ¿Tiene unidades de fuerza? ¿Dice cosas razonables, como cuánto debería valer la fuerza para ángulos de 0 y 90 grados? ¿Podés pensar dos o tres preguntas más para hacerle a esa expresión y estar seguro de que es el resultado correcto? ¿Podrás explicar para qué puso el autor del problema una velocidad hacia arriba?   Ricardo Cabrera
DESAFIO: Resolver este problema con un SR que tenga un eje vertical y otro horizontal, para ambas situaciones: la de aceleración cero y distinta de cero.  
Algún derecho quedó sin reservar. No se permite su reproducción sin citar la fuente. Ojito. Última actualización oct-06. Buenos Aires, Argentina.