NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Leyes de Newton, vínculos)
|
|

|
 |
31) La base de un plano inclinado mide 12 m y la altura 5 m. Desde la cúspide del plano,
parten simultáneamente, desde el reposo, dos móviles, uno por el plano inclinado y el otro
en caída libre. Despreciando los rozamientos:
a) Calcular el tiempo que cada uno tarda en llegar a la base del plano.
b) Hallar la velocidad que tiene cada uno al llegar a la base del plano. |
|
| Como casi siempre, todo buen ejercicio de física, incluye una buena cuota de geometría, álgebra, trigonometría, agrimensura, corte y confección, ética y deontología... Como es casi seguro que lo vamos a necesitar, calculemos el ángulo de inclinación del plano y la longitud del recorrido sobre el plano, así no interrumpimos después, durante el desarrollo físico. |
|
|
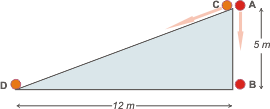 |
El recorrido CD podés calcularlo por Pitágoras: 12²+5² = CD², de donde resulta que CD = 13 m
El ángulo de inclinación es aquel cuya tangente vale 5/12, de donde resulta que α = 22,6º |
|
|
|
Empecemos con el cuerpo que cae libremente por la vertical. Voy a usar un SR positivo hacia arriba con el 0 en el piso, ¿Ok? (Lo hago sólo por llevarte la contra).
y = 5 m – 5 m/s² t ²
v = – 10 m/s² t
Si a esas ecuaciones le pedimos que hablen del instante en que el móvil llega al piso...
0 m = 5 m – 5 m/s² tB²
vB = – 10 m/s² tB
De la primera despejo tB, y lo que da lo meto en la segunda. |
|
|
|
|
|
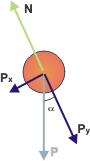
La fuerza que acelera al móvil es la componente del peso paralela al plano. Y la aceleración vale a = g sen α. Si tenés dudas acerca de ésta aceleración podés repasar el asunto en este otro ejercicio.
a = g . 5/13 = 3,85 m/s²
Las ecuaciones que describen el movimiento de este cuerpo son:
z = 13 m – 1,92 m/s² t ²
v = – 3,85 m/s² t
|
|
|
|
Si te cuesta entender el asunto de la descomposición de la fuerza peso, te recomiendo leer este apunte. |
Te habrás dado cuenta que elegí un SR con el cero en el piso y ascendente sobre el plano inclinad... sólo para enojarte.
Ahora le pido a esas dos ecuaciones que se refieran al instante en que el móvil llega al piso:
0 m = 13 m – 1,92 m/s² tD²
vD = – 3,85 m/s² tD
Y hago lo mismo que antes: despejo tD, y lo reemplazo en la otra. |
|
|
| |
tD = 2,60 s, vD= – 10 m/s |
|
|
|
|
Te habrás dado cuenta de que ambos llegan con la misma velocidad (en módulo). Si bien el que desliza por el plano inclinado tarda bastante más que el otro... cuando llega al piso lo hace con la misma velocidad final.
Nota: este mismo ejercicio se puede resolver haciendo consideraciones de energía. De ese modo es mucho más fácil. Lo tenés resuelto acá. |
|
|
|
|
 |
DESAFIO: Hacer una demostración de que la velocidad final debe ser la misma siempre, independientemente de la inclinación del plano.
|
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Última actualización jun-08. Buenos Aires, Argentina. |
|
|
|

