 |
NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Leyes de Newton, plano inclinado)
|
|

|
| |
| Plano inclinado. Acá tenemos otro motivo que aparece metido ad-infinitum en innumerables ejercicios de dinámica en este curso. Estate atento que voy a remarcar los errores más comunes que cometen los estudiantes cuando lo enfrentan sin haberlo practicado. |
 |
|
Se trata de un cuerpo apoyado sin rozamiento sobre un plano inclinado un cierto ángulo, α, respecto a la horizontal. Es obvio que ese cuerpo acelerará hacia abajo con una cierta aceleración, a, que debemos averiguar.
Por supuesto, en dinámica, todo comienza con un DCL.
|
| |
 |
Recordá que enfrentamos la situación ideal en la que no hay rozamiento entre el cuerpo y el plano en el que desliza.
Luego, hay sólo 2 fuerzas actuando sobre el cuerpo. Su peso, P, vertical, lógicamente. El apoyo en el plano inclinado, A, (que es perpendicular, o normal, al plano) y ninguna otra más. Los errores típicos de tus compañeros (no tuyos) son agregar fuerzas que no existen, por ejemplo... "la fuerza de la velocidad" (una interacción misteriosa creada por duendes muy veloces) y "la normal" (una interacción omnipresente sobre todos los cuerpos del universo). No inventes. |
|
|
|
| Esas dos fuerzas no tienen la misma dirección, de modo que debemos elegir un sistema de referencia, SR, para poder plantear la ecuación de Newton. Cualquier SR es igualmente válido, pero un SR con un eje paralelo al plano inclinado (y a la aceleración) nos va a resultar muy ventajoso. |
|
|
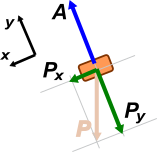 |
No es casualidad que haya elegido ese SR. El eje x, siempre que puedo, lo hago coincidir con la dirección y sentido de la aceleración del movimiento, entonces en el eje y la aceleración es cero.
Y ahora aplicamos la 2da. Ley de Newton por separado para cada uno de los ejes. Empecemos con la dirección paralela al plano. |
|
|
|
ΣFx = m ax = m a
hay una sola fuerza en esa dirección,
Px = m a
Ahora vamos con la dirección normal al plano:
ΣFy = m ay = 0
A – Py = 0
En este problema en particular esta última ecuación no aporta gran cosa. Pero la de x sí.
Y acá es donde un buen porcentaje de estudiantes comete el error fatal. ¿Cuál es la relación entre el peso y sus componentes? |
|
|
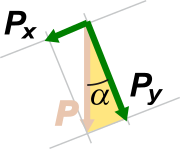 |
Mirá el triangulito que quedó formado y que sombreé en amarillo. Es rectángulo, no cabe duda. Px y Py son los catetos y P es la hipotenusa. El ángulo α no es otro que el ángulo de inclinación del plano inclinado. (Si no entendés por qué α es ése que marqué y no el que está al lado de Px, te recomiendo que mires este artículo del maestro Ciruela). De modo que
Px = P . sen α
Py = P . cos α
|
|
|
Si la descomposición de P no te convence... te recomiendo que recurras a esta ayuda.
|
Si reemplazo Px en la ecuación x de Newton nos queda...
P . sen α = m . a
recordando que...
P = m . g
m . g . sen α = m . a
de donde:
g . sen α = a
|
|
|
|
|
|
|
|
|
DISCUSION: La primer pregunta que nos hacemos siempre es: ¿tiene las unidades correctas este resultado? Sí, por supuesto, tiene unidades de aceleración ya que es el producto entre g, que es una aceleración (10 m/s²), y sen α, que como toda función trigonométrica es adimensional, no tiene unidades. Vamos bien.
¿Y tiene sentido físico el resultado? Y... parece que sí, fijate, si α valiera cero estaríamos frente a un plano horizontal, ahí la aceleración debe valer cero, y es justo lo que dice el resultado ya que sen 0º = 0. Si α crece, sen α también crece; o sea cuanto más inclinado esté el plano mayor será la aceleración lo cual parece muy lógico.
¿Y si α valiera 90º? El cuerpo estaría cayendo por un precipicio vertical con una aceleración igual a g, tal como dice el resultado ya que sen 90º = 1. Viste que siempre un planteo no numérico es mucho más aleccionador que uno numérico. |
|
|
| DESAFIO: ¿Podría el cuerpoestar subiendo por la pendiente y sin que nadie ni nada lo empuje hacia arriba? (R: sí) ¿Cómo? ¿Cuánto valdría su aceleración? |
|
 |
| Algunos derechos reservados (no es que sean tímidos, callados, modestos...).
Se permite su reproducción citando la fuente. Última actualización set-21. Buenos Aires, Argentina. |
|
|
|

