Movimiento oscilatorio armónico simple (MOAS)

El movimiento oscilatorio armónico simple (MOAS) que también te va a aparecer en muchos lados como MAS o como MOA, es uno de los movimientos más importantes del universo. Las oscilaciones naturales, las ondas que viajan, las vibraciones de casi cualquier cosa... se mueven de esta manera.

Cuando arranquemos a resolver los ejercicios de MOAS vas a encontrar que aparece en su lenguaje descriptivo los mismos términos que aparecían en el movimiento circular uniforme (MCU): frecuencia, período, etcétera. ¡Y significan lo mismo!

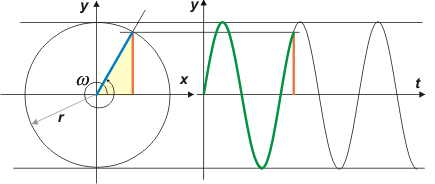
Para explicártelo, preparé este esquema de la relación. En la izquierda tenés una circunferencia que podría ser la trayectoria de un móvil animado de un MCU... con su radio, r, y su velocidad angular, ω.

Si interpretás bien el esquema, entenderás que el móvil ya dió una vuelta entera y un poquito más (menos de un cuarto), ¿estamos de acuerdo? Bien, la trayectoria circular podemos referirla a un par de ejes cartesianos x e y, como se muestra en el esquema. El gráfico de la derecha es, justamente, el gráfico de posición-tiempo -que ya conocés y practicaste hasta el cansancio en el capítulo de cinemática-, que muestra solamente el desplazamiento del móvil en la dirección del eje y. (Podría haber hecho lo mismo pero en la dirección x).

Ese apartamiento en función del tiempo se puede expresar fácilmente de esta manera:

y = r sen (ωt)

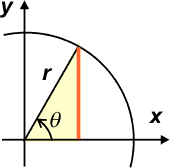
La explicación es muy sencilla. Mirá atentamente el detalle del triángulo que queda formado en cada instante entre el radio que marca la posición del móvil del MCU (te lo sombreé en amarillo) y las direcciones x e y.

Supongamos por un momento, para simplificar las cosas, que en el instante igual a 0 s el ángulo valía 0... entonces:

θ = ωt

con lo que llegamos a la ecuación de allá arriba. Generalicemos un poco: supongamos que no coinciden los ceros del tiempo con los del ángulo (no te olvides que estos ceros son arbitrarios, convencionales). Sea entonces φ el ángulo "inicial" (también llamado de fase inicial o ángulo de fase), nos queda:

y = r sen (ωt + φ)

Y análogamente:

x = r cos (ωt + φ)

De modo que si tenemos un movimiento oscilatorio con esta pinta (senoidal o cosenoidal) la podemos asociar a un movimiento circular uniforme ficticio, irreal, pero que echa enorme luz sobre nuestro movimiento oscilatorio y facilita los cálculos enormemente. Lógicamente, no hablaremos de radio (ficticio), sino de amplitud (la magnitud real de la oscilación)... Tampoco hablaremos de velocidad angular sino de pulsación...

La pulsación de una onda (como la velocidad angular en un MCU) está relacionada sencillamente con la frecuencia del movimiento:

ω = 2π . f = 2π / T

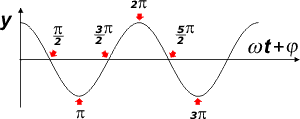
Fijate qué fácil es -ahora- encontrar los puntos notables de una oscilación...

En los MOAS A, ω y φ son constantes. También lo son la frecuencia y el período. (Como lo son en su respectivo movimiento circular asociado ficticio).

Uno de los aspectos más interesantes de los movimientos armónicos es que la frecuencia de oscilación, o pulsación, ω, no depende de la amplitud del movimiento sino de la estructura del sistema físico. Galileo fue el primer que se dio cuenta que cada sistema tiene una única frecuencia natural de oscilar o vibrar (nuestro ω) que dependen en cada caso de la dureza, o de la masa, o del tamaño de los objetos o sistemas que vibran. Te doy algunos ejemplos:

Un cuerpo unido a un resorte:

ω = (k/m)^½

Donde k es la constante elástica del resorte, m la masa del cuerpo y el exponente ^½ es lo mismo que raíz cuadrada (no existe el símbolo de raíz en el lenguaje html, de internet).

Un péndulo simple (amplitudes pequeñas):

ω = (g/l)^½

Donde g es la aceleración de la gravedad y l es la longitud del piolín del péndulo.

Una cuerda que vibra (por ejemplo la de un instrumento de cuerdas):

ω = (T/ λ)^½

Donde T es la tensión de la cuerda y λ es la densidad lineal de masa.

Lo interesante de todo esto no es una simple curiosidad matemática. Resulta que los movimientos oscilatorios más importantes del universo ¡son armónicos y simples! De modo que para describirlos se utilizan estas herramientas matemáticas.

CHISMES IMPORTANTES

• La importancia del MOAS trasciende sus fronteras, ya que como lo demostró un señor llamado Fourier, cualquier oscilación periódica puede ser considerada como una superposición de varios movimientos oscilatorios armónicos simples.
• La ecuación del MOAS facilita enormemente el estudio de la cinemática del movimiento... Si recordás que la función velocidad es la derivada primera de la de posición; y la de aceleración la segunda, hallamos rápidamente...
  
          x = A cos (ωt+φ)
  
          v = – A ω sen (ωt+φ)
  
          a = – A ω² cos (ωt+φ)
  
  Veo que ya te olvidaste cómo se deriva... pero no tiene importancia; lo que sí la tiene es que puedas discutir físicamente estos hallazgos.
  
• Las oscilaciones eléctricas (aquellas que, por ejemplo, producen la corriente alterna) también se describen perfectamente con un MOAS.
  

• ¿Cómo describirías vectorialmente (en un par de ejes cartesianos) el movimiento de una partícula animada de un MCU?
• ¿Qué será un MOA amortiguado?
• Tiene sentido que cada sistema físico (mecánico, por ejemplo) tenga una y sólo una frecuencia (o modo de vibración) natural?
• ¿Qué se te ocurre con la palabra resonancia?
• Acordate de la expresión del período del movimiento del péndulo simple ¿te animás a encontrar la velocidad angular del MCU asociado?