NO ME SALEN
EJERCICIOS RESUELTOS DE FÍSICA
(Movimiento de tiro oblicuo)
|
|

|
| Adicional No me salen 8.3 - Se lanza un objeto desde el piso, logrando un alcance de 30 metros. El ángulo con el que se lanza el objeto se desconoce. El radio de curvatura en la parte más alta del recorrido vale 10 metros. Calcular la velocidad inicial y el ángulo con la que fue lanzado el objeto. * |
|
Este interesante ejercicio de tiro oblicuo incluye un concepto que no siempre se tiene a mano: radio de curvatura... no es para amargarse. Primero te explico de qué se trata y qué papel juega en este asunto, y después lo resolvemos. |
|
|
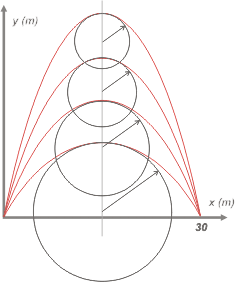 |
En este gráfico representé 4 tiros oblicuos. Sus trayectorias son las curvas rojas. Como vos ya sabés, son arcos de parábola.
Representan 4 tiros con el mismo alcance, 30 m, tal como indica el enunciado. Se diferencian en la altura del vuelo. Lógicamente aquel que llega más arriba habrá sido lanzado con una velocidad mayor y apuntando más hacia arriba... y el que alcanza menor altura se habrá lanzado con menos velocidad y más hacia abajo.
Pero la característica a nosotros nos interesa en este caso es que cuanto más arriba vaya el tiro más angulosa es la trayectoria en su punto más alto (en su vértice diría, un matemático). Las 4 circunferencias que parecen tener pegadas en la concavidad superior las 4 parábolas son las circunferencias osculatrices, y el radio de esas circunferencias el radio de curvatura, del que habla el enunciado. |
|
|
|
| Como ves, cuanto más alto llega el tiro, más cerrada es la parábola y menor el radio de curvatura. Hay un continuo que va desde el tiro más bajo al tiro más alto... de modo que habrá una y sólo una trayectoria cuyo radio de curvatura valga 10 m, y es esa, justamente, la del tiro que nos interesa. |
|
|
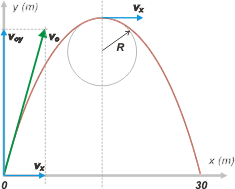 |
Existe una relación muy sencilla entre el radio de curvatura, R, y la velocidad del móvil en el punto donde la circunferencia osculatriz toca a la trayectoria (en nuestro caso, el vértice de la parábola).
R = v²/g
de donde
v = (R . g)½
Pero esta velocidad no es otra que la velocidad de desplazamiento horizontal y constante del tiro oblicuo, vx, ya que se trata, justamente del punto más alto. |
|
|
|
Calculemos su valor, ya que estamos...
vx = (10 m . 10 m/s²)½ = 10 m/s
El resto es un problema de tiro oblicuo común y silvestre. Tomando como instante de tiempo inicial 0 s, y como posición inicial en x y en y 0 m y un SR que apunta hacia arriba, las ecuaciones que describen el tiro son estas 3: |
|
|
| |
x = 10 m/s . t |
|
| |
y = voy . t — 5 m/s² t² |
|
| |
vy = voy— 10 m/s² t |
|
|
|
PASO DOS
ARMAR
LAS ECUACIONES |
| A esas ecuaciones les pedimos que hablen del alcance: |
|
|
| |
30 m = 10 m/s . tA |
[1] |
| |
0 m = voy . tA — 5 m/s² . tA² |
[2] |
| |
vy = voy — 10 m/s² tA |
[3] |
|
|
PASO TRES
USAR
LAS ECUACIONES |
La ecuación [3] no aporta información en este ejercio, y no hace falta usarla. Las otras dos sí. De la [1] despejo y calculo tA:
tA = 3 s
Con ese valor voy a la [2], y despejo y calculo voy
voy = 15 m/s
Ya tengo las componentes de la velocidad inicial del tiro (vx y voy), que es lo que pide el enunciado; me basta con componerlas utilizando Pitágoras
vo = (vx² + voy²)½
|
|
|
| |
|
|
Y el ángulo de tiro, α, lo hallamos utilizando la función inversa de la tangente, también llamada arcotangente, arc tg (en criollo: el ángulo cuya tangente vale...),
α = arc tg (voy / vx )
|
|
|
|
|
|
|
|
|
| (*) Este ejercicio perteneció al primer examen parcial de Física I del ITBA de 2010 y me lo envió gentilmente mi amigo Gastón Máspero. |
|
|
|
DESAFIO: ¿Cuánto valdrá el radio de la circunferencia osculatriz inicial? ¿Por qué se llamará osculatriz? |
|
 |
| Algunos derechos reservados.
Prohibida su impresión en impresoras berretas. Se permite su reproducción citando la fuente legítima, o sea, este sitio. Última actualización abr-10. Buenos Aires, Argentina. |
|
|
| |




