NO ME SALEN
SOLVED PHYSICS EXCERCISES FROM THE CBC
|
|

|
Adiotional: No me salen 7.17* - A plave flies to the West at 600km/h for 3 hours and then to the North with the same speed, for two 2 hours. It´s average speed vector, in a coordinate system (as sthe one shown below) is:
|
a) – 600 km/h î + 600 km/h ĵ
b) – 721 km/h î + 1081 km/h ĵ
c) – 200 km/h î + 300 km/h ĵ
d) – 849 km/h î + 849 km/h ĵ
e) – 432 km/h î + 432 km/h ĵ
f) – 360 km/h î + 240 km/h ĵ |
|
|
|
|
î and ĵ are vectors of modulus 1, also called "Versors", their objetive is to join the vectorial characteristics of a number and tell where it is pointing to. Usually it is portrayed with a little hat or a little comma above (replacing the typical i and j) . Versor î has the same direcction and sense in the x axis, as the ĵ versor in the y axis.
This beautifull problem caused a real havoc. An exam was taken and only the 17,4% of the students (deducting the 1/6 that just guessed). Almost all the students tried to solve it in a swipe, with a sigle calculation, with a formula (what a shamefull concept about physics), and very few -a 17,4% - took the job of assembling graphs and schemes. Let´s begin there. |
|
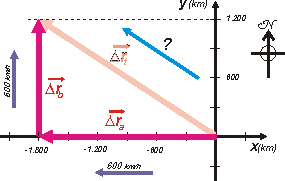
The first displacement, to the West, is done at 600 km/h and it lasted for 3 hours. That displacement, Δra, was 1.800 km. I don´t even need to explain that.
With the same reasoning, the second displacement, Δrb, wich lasted for 2 hours, was 1.200 km long.
The total displacementl, Δrt, can be calculated by Pitágoras. |
|
|
|
And it´s equal to Δrt = 2.163 km, but to travel through it, it took 5 hours. This way, if we wanted to find the modulus of the averages speed´s total vector, the one in light blue, we should have to divide the total displacement by the total time interval.
vmt = Δrt / Δtt
vmt = 2.163 km / 5 h
vmt = 433 km/h
But this problem does not offer us this value as a possible answer. The total average speed vector is expressed in function of it´s orthogonal components, we could call them vmtx y vmty.
A less ``piggy´´ way to find the answer is to search wich of the offered pairs in the answers, match with the Pitagorical sum (it´s vectorial sum), that is vmt = 433 km/h. And there is only one. But there are other more honorable methods.
The total average speed in the X direction, vmtx, is goint to be equal to: |
|
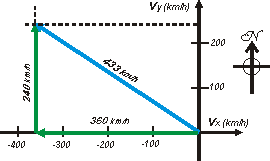
vmtx = Δra / Δtt
vmtx = -1.800 km / 5 h
vmtx = -360 km/h
And similarly:
vmty = Δrb / Δtt
vmty = 1.200 km / 5 h
vmty = 240 km/h
This way, the answer is: |
|
|
|
| |
vmt = – 360 km/h î + 240 km/h ĵ |
option f) |
|
|
| CHALLENGE: solve the problem this way: find the angle formed between the total displacement and the x axis. Then, with the sinus and the cosine of that angle, decompose the total average speed´s vector in it´s x and y components, and verify that this way, you reach the same conclusion as mine. |
|
| |
 |
| |
| *Excercise copied from the first exam of physics, in Universitary City CBC, the first quarter of 2006. |
|
|
| |
|
| Some Rights Reserved. Not allowed to be copied without naming either the author or this source material. Those ones not obeying these rules will be sentenced to hard labor in the Antarctica. Translated by Santi Pisci. Last updated ago-15. Buenos Aires, Argentina. |
|
|
|

