NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA
(Movimiento relativo)
|
|

|
 |
NMS c7.09- Felipe mide el tiempo de caída de una
moneda que tiene sujeta con sus dedos a una altura
h del piso de un ascensor, cuando el mismo
está en reposo. Repite la experiencia cuando el
ascensor sube con velocidad constante de 2 m/s,
y nuevamente la realiza cuando desciende a
2 m/s, siempre desde la misma altura h. ¿En cuál
de las experiencias registró un intervalo de tiempo
mayor? |
|
¿Hiciste el problema Nc3.02 de Jaimito y una botella? Pegale una ojeada, o resolvelo, si no lo hiciste. Felipe no es Jaimito, pero acá ocurre lo mismo que en muchos problemas de movimiento relativo, a saber, que los podés resolver del modo corriente... pero si los resolvés haciendo las consideraciones de relativo, resulta más económico, y mejor.
Para que te vayas ambientando te hice un dibujito que vamos a usar como esquema, y nos va a servir para las tres situaciones descriptas en el enunciado. |
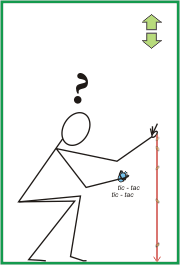 |
El flaquito ése es Felipe, con un cronómetro en la derecha y jugando con moneditas con la izquierda. Como tiene un cronómetro que le permite poner el cero en el inicio de la caída, en lugar de considerar intervalos voy a considerar instantes de la caída (supongo que tenés claro que Δt es igual a t cuando t0 es igual a 0).
El modo tradicional de resolver el problema sería plantearlo como un encuentro entre la moneda y el piso del ascensor, que puede estar quieto, subir a velocidad constante o bajar también a velocidad constante.
La ecuación de la moneda (MRUV) sería
y = h + vM . t – 5 m/s² . t²
y la del piso del ascensor (MRU)
y = vA . t
|
|
|
|
En el encuentro la altura de ambos será la misma, por lo tanto puedo igualar los segundos miembros de ambas ecuaciones. Quedaría una cosa así:
vA . te = h + v0M . te – 5 m/s² . te²
y acá viene el pase mágico: ¡tenés que apiolarte de que la velocidad inicial de la moneda es la misma para ambos móviles! ¡Patrañas!, pensarás vos... el enunciado dice que Felipe suelta la moneda... no que la arroja (tampoco dice "suelta" pero lo da a entender)... y desde que tenías 5 años te enseñaron que "suelta", o "deja caer", significa velocidad inicial igual a cero. Temo que no entendiste del todo correctamente... Es cierto que "suelta" significa velocidad inicial nula, ¡pero con respecto a los dedos que sueltan!
Vamos de otra manera: cuando el ascensor sube a 2 m/s la mano de Felipe también sube a 2 m/s, y la moneda de la mano de Felipe también sube a 2 m/s. Y pasará lo mismo en cualquier otra situación. De modo que cuando Felipe suelta la moneda, en ese preciso instante, la moneda tendrá la misma velocidad que el ascensor... valga lo que valga. O sea:
vA = v0M
eso hace que dos términos se cancelen, y te queda...
0 = h – 5 m/s² . te²
de donde el tiempo en llegar al suelo valdrá siempre lo mismo, es independiente de lo que haga el ascensor (mientras sólo se mueva a velocidad constante), y será
|
|
|
| |
te = (2h/g)½ |
(raíz cuadrada de 2h/g) |
|
|
|
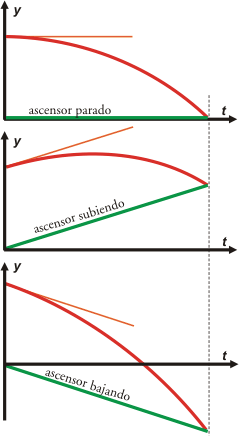 |
Acá te hice tres gráficos en la misma escala de tiempo. La posición de la moneda en rojo, y la del piso del ascensor en verde. Quieto, subiendo y bajando, respectivamente.
Prestale atención al detalle de esa rayita naranja que coloqué sobre la parte inicial de la gráfica de la moneda. La tracé exactamente tangente a la curva. O sea que el tramo inicial de la curva, y la rayita ésa, tienen la misma inclinación. Acordate que la inclinación de la curva posición-tiempo nos revela la velocidad de móvil.
Fijate también que la rayita es paralela a la gráfica de posición-tiempo del piso del ascensor.
Estos detalles no son casuales; nos indican que los gráficos son gráficos No me salen, que vienen con garantía de cinco años, y que nos muestran que la velocidad inicial de la moneda al dejarla caer es igual a la velocidad del ascensor, o sea... nada*.
Y ahora vamos a resolver la cuestión con consideraciones galileanas. |
|
|
|
Voy a llamar VMA, a la velocidad de la moneda vista por Felipe, un habitante del ascensor. VAT será la velocidad del ascensor vista por un terrícola parado en planta baja (u otro piso cualquiera, eso es a gusto tuyo). Y VMT, la velocidad de la moneda vista por el terrícola que, obviamente, debe tener vista de rayos X. Galileo estableció que:
VMT = VMA + VAT
Las velocidades que nos interesan son las que tiene la moneda antes de ser soltada. De modo que para nuestro análisis: VMA = 0, de lo que concluimos que
VMT = VAT
que no es otra cosa que lo que razonamos antes cuando planteamos el encuentro entre dos cuerpos independientes, ambos observados desde Tierra. THE END. | | |
Discusión: Ni tirar monedas, ni ningún otro experimento (esto es lo que le interesaba a Galileo) sirve para decidir si un espacio (en este caso el ascensor) se está moviendo uniformemente o si está quieto. Todavía más, te digo: ES LO MISMO. |
|
|
*Nada. Todo, algo, nada, eso, nada. Muletilla utilizada por los que tienen nada en la cabeza. "Cuando mi novio va a la pileta... nada, nada. Después, como queda muy cansado, si salimos a la noche... nada, nada". |
|
 |
| DESAFIO: buscá una expresión que te permita calcular la velocidad con que llega la moneda al piso del ascensor, vista por el chabón de planta baja. |
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Felipe... ¿es millonario? Última actualización may-07. Buenos Aires, Argentina. |
|
|
| | | |
|

