 |
NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA
(Movimiento relativo)
|
|

|
 |
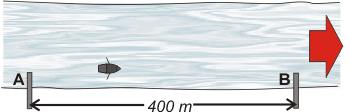
NMS c7.04 - Entre los muelles A y B, que están en la misma orilla de un canal rectilíneo, hay una distancia de 400 m. Un bote de remos tarda 40 segundos en ir de A hasta B, y 50 segundos en regresar. Considerando constantes los módulos de las velocidades del bote respecto del agua y de la corriente respecto a la orilla, hallar el valor de los mismos. |
|
Acá tenemos dos movimientos; el primero es el bote yendo de A hacia B, y el segundo es el regreso. Y ambos son movimientos efectuados en un medio que tiene movimiento propio: el río. O sea, tenés dos problemas en uno. Mirá el esquema: te hice los dos movimientos por separado, pero usé el mismo sistema de referencia.
|
| |
 |
|
|
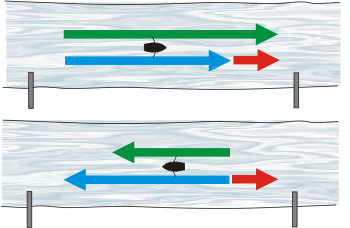
Para cada uno de los movimientos se cumple que la velocidad del bote (nuestro móvil), medida desde la orilla (desde la Tierra), es igual a la velocidad del bote en el agua más la velocidad del agua, o sea la del río. ¿Identificaste a los tres protagonistas de esta historia? Son siempre los mismos. Acá, como subíndice, usé B (de bote) en lugar de M (de móvil).
VBT = VBR + VRT
Acá lo voy a aplicar dos veces, una para el movimiento de la ida y otra para la vuelta.
VBT ida = VBR + VRT
VBT vuelta = VBR + VRT
La velocidad del río no cambia durante los dos movimientos, por eso no le puse subíndice ida ni vuelta. Lo mismo para la velocidad del remero (que se supone que no está más cansado a la ida que a la vuelta). |
|
|
 |
|
|
Fijate que el largo de los vectores rojo y azul es en los dos casos el mismo.
VBT ida = ΔXida / Δtida = 400 m / 40 s = 10 m/s
VBT vuelta = ΔXvuelta / Δtvuelta = – 400 m / 50 s = – 8 m/s
Es fácil entender que AB = – BA, y por lo tanto VBT ida es positivo y VBT vuelta es negativo. No tan sencillo es razonar que en un caso el bote va a favor de la corriente y en el otro en contra. O sea: VBR ida = – VBR vuelta.
Si reescribimos las ecuaciones metiendo esta información... |
|
|
 |
10 m/s = VBR + VRT
- 8 m/s = – VBR + VRT |
|
|
Hoy es nuestro día... encontramos un sistema de dos ecuaciones con dos incógnitas. El resto es álgebra. Es fácil: sumemos ambas ecuaciones miembro a miembro
2 m/s = 2 VRT
|
|
|
| |
| VRT = 1 m/s |
la velocidad del río |
|
|
|
|
| Con ese valor vamos a las dos ecuaciones y verificamos que dan igual. |
|
¿Tenés ganas de leer algo copado? |
| |
| VBR = 9 m/s |
la velocidad del bote |
|
|
|
Me queda una duda, ¿ese bote será realmente un bote? ¿Una chalupa tal vez? ¿Un chinchorro quizás? ¿Una falúa? ¿Un esquife, un batel, una balandra, una gabarra, un caique, una chalana, una yola...? ¿Qué será?
DESAFIO: ¿qué pasará el día que el río tenga una crecida y avance a 9 m/s?
|
|
 |
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Este material es absolutamente gratuito; el mejor pago para el trabajo que me tomé es que aceptes el DESAFIO y lo resuelvas. Y si no... te espero en la esquina. Última actualización set-06. Buenos Aires, Argentina. |
|
|
| |
|

