| home | | | más de cinemática | | | otros temas de Física | | | lecciones del maestro Ciruela | | | tonterías | | | @ |
| NO ME SALEN PROBLEMAS RESUELTOS DE FÍSICA (Tiro oblicuo) |
|
||||||||||||
|
|||||||||||||
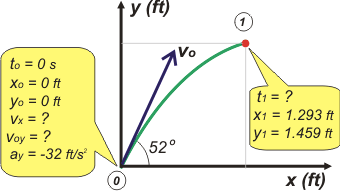
Pero qué terrible... ¡en este ejercicio las longitudes están medidas en pies! ¡Me quiero morir! ¿Será muy diferente? Es lo mismo... un día de estos voy a proponer un ejercicio que mida las longitudes en camellos y los tiempos en escupidas. Las velocidades se medirán en camellos por escupidas, y las aceleraciones en camellos por escupidas cuadradas. No perdamos tiempo, este ejercicio sale en una escupida. Como cualquier ejercicio de cinemática, arrancamos con un esquema: |
|||||||||||||
|
|||||||||||||
Habrás notado que el símbolo de pie es ft. Un pie es algo así como 30 centímetros. Para ser más preciso:
Sigamos con el ejercicio. ¿Cuántas ecuaciones horarias describen el movimiento? Tres, porsupu, como todo TO. Para hallarlas basta con reemplazar las constantes (to , xo , yo , vx , voy , y g) de las ecuaciones generales de los tiros oblicuos:
En el esquema, en el globito que habla del punto 0, están todas las constantes que necesitamos para armar las ecuaciones que describen el movimiento del cuerpo. Si hubieses nacido en Estados Unidos sabrías que la aceleración de la gravedad vale g = 32,152 ft/s². Pero como no lo sabés, tendrás que hacer el pasaje de unidades.
|
|||||||||||||
Ahora les pedimos a las 3 ecuaciones que hablen del punto de interés, el 1, en el que el proyectil alcanza la posición indicada en el enunciado. |
|||||||||||||
|
Estas son las ecuaciones especializadas para el instante que a vos te interesa. | ||||||||||||
Acá terminó la física del problema... lo que resta es álgebra. Veamos qué sorpresas nos depara el álgebra. Pero acordate... esto ya no es Física. Las dos primeras ecuaciones tienen las dos mismas incógnitas, y la tercera ecuación no aporta nada (no hay dato ni incógnita interesante), así que no la voy a usar. Despejo t1 de la primera ecuación: |
|||||||||||||
|
|||||||||||||
| Y lo meto en la [2] | |||||||||||||
|
|
||||||||||||
| Tené presente que cos 52° = 0,6157 y que sen 52° = 0,7880. | |||||||||||||
|
|||||||||||||
vo² = 360.339 ft²/s² |
|||||||||||||
|
|||||||||||||
Lanzamiento a 600 pies por segundo. |
|||||||||||||
DESAFIO: Rehacer todo en metros. |
 |
||||||||||||
|
|||||||||||||