 |
NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA
(Tiro oblicuo)
|
|

|
NMS c5.29* - Desde un avión que vuela horizontalmente a 250 km/h se deja caer un paquete, que llega al piso luego de 5 s.
a) determinar la altura a la que vuela el avión.
b) Calcular la velocidad (módulo y ángulo) con que el paquete llega al piso, de acuerdo con un observador fijo a la Tierra.
|
|
Las palabras del enunciado se deja caer aluden a que el paquete se suelta (no se tira), que por lo tanto, su velocidad inicial es igual a la del avión: una velocidad horizontal de 250 km/h, o lo que es lo mismo: 69,44 m/s. Se trata entonces de un tiro horizontal.
|
| |
|
|
¿Cuántas ecuaciones horarias describen el movimiento? Tres, porsupu, como todo TO. Para hallarlas basta con reemplazar las constantes (to , xo , yo , vx , voy , y g) de las ecuaciones generales de los tiros oblicuos:
x = xo + vx ( t – to )
y = yo + voy ( t – to ) + ½ g ( t – to )²
vy = voy+ g ( t – to )
En el esquema, en el globito que habla del punto 0, están todas las constantes que necesitamos para armar las ecuaciones que describen el movimiento del cuerpo.
x = 69,44 m/s . t
y = 5 m/s² . t²
vy = 10 m/s². t
|
|
|
Ahora pidámosle a esas ecuaciones que hablen del momento en que el paquete llega al piso, P. |
|
|
 |
xP = 69,44 m/s . 5 s |
[1] |
|
| yP = 5 m/s² . 25 s² |
[2] |
|
| vyP = 10 m/s². 5 s |
[3] |
|
|
|
Estas son las ecuaciones especializadas para el instante que a vos te interesa. |
Acá terminó la física del problema... lo que resta es álgebra. A la ecuación [2] le podemos preguntar cuánto recorrió verticalmente el paquete desde que fue soltado, o sea, la altura a la que viaja el avión.
yP = 5 m . 25
|
|
|
|
|
|
Para saber con qué velocidad llega al piso le preguntamos a la ecuación [3] cuánto vale su componente vertical en ese instante:
vyP = 50 m/s
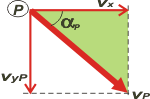
Acordate que la velocidad horizontal se mantiene constante. Por lo tanto, recordando el teorema de Pitágoras, la velocidad real cuando llega al piso, vP, valdrá:
vP² = vx² + vyP²
vP² = (69,44 m/s)² + (50 m/s)²
|
|
|
| |
vP = 85,57 m/s |
respuesta b) |
|
|
|
| Y para saber con qué ángulo impacta en el piso, recordá que la tangente de un ángulo es el cociente entre el cateto opuesto sobre el cateto adyacente (en un triángulo rectángulo, como es el caso). |
|
|
tg αP = vyP / vx
tg αP = 50 m/s /69,44 m/s
tg αP = 0,72
Haciendo la función inversa... |
 |
|
|
|
|
|
|
| La ecuación [1] ni la necesitamos. |
|
|
*Este ejercicio perteneció al primer examen parcial tomado en octubre de 2013. |
|
|
DESAFIO: ¿Cuánto se desplaza el avión mientras cae el paquete? |
|
 |
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. También se permite que sea sin reproducción... ¿se comprende? Última actualización oct-13. Buenos Aires, Argentina. |
|
|
| |
|

