 |
NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA
(Tiro oblicuo)
|
|

|
NMS c5.28 - Se dispara un proyectil desde el piso (xo = 0, yo = 0) de modo que supera una valla de altura H, situada a una distancia horizontal D del punto de lanzamiento. El ángulo de disparo, α, medido respecto a la horizontal, para que el proyectil alcance su altura máxima al llegar a la valla y pase rasante a ella, debe cumplir:
a) tg α = 2H/D b) sen α = H/D c) cos α = H/D
d) tg α = H/2D e) cos α = D/H f) tg α = 2D/H |
|
Otro ejercicio que parece estrambótico y no es más que una aplicación sencilla, rutinaria, si adherís al método que te propone No me salen.
Como cualquier ejercicio de cinemática, arrancamos con un esquema: |
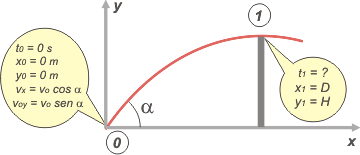 |
Acordate que:
vx = vo cos α
voy = vo sen α
Y que si elegimos un SR que apunta hacia arriba la gravedad es negativa. |
|
|
|
¿Cuántas ecuaciones horarias describen el movimiento? Tres, porsupu, como todo TO. Para hallarlas basta con reemplazar las constantes (to , xo , yo , vx , voy , y g) de las ecuaciones generales de los tiros oblicuos:
x = xo + vx ( t – to )
y = yo + voy ( t – to ) + ½ g ( t – to )²
vy = voy+ g ( t – to )
En el esquema, en el globito que habla del punto 0, están todas las constantes que necesitamos para armar las ecuaciones que describen el movimiento del cuerpo.
x = vo cos α . t
y = vo sen α . t – 5 m/s² . t²
vy = vo sen α – 10 m/s² . t
|
|
|
Ahora les pedimos a las 3 ecuaciones que hablen del punto de interés, el 1, en el que el proyectil pasa rasante justo por arriba del muro.
Posición más alta significa que la velocidad vertical en ese punto vale cero: justo en ese instante el proyectil no está subiendo ni bajando. |
|
|
 |
D = vo cos α . t1 |
[1] |
|
| H = vo sen α . t1 – 5 m/s² . t1² |
[2] |
|
| 0 = vo sen α – 10 m/s² . t1 |
[3] |
|
|
|
Estas son las ecuaciones especializadas para el instante que a vos te interesa. |
Acá terminó la física del problema... lo que resta es álgebra. Y es bastante sencilla, tenés que probar vos... debe haber varios caminos posibles. Acá va el mío:
De la ecuación [3] despejo t1 que es una incógnita que no nos interesa. |
|
|
|
|
|
| Y lo meto en la [1] |
|
|
| |
| D = |
|
vo² sen α . cos α |
|
|
| 10 m/s² |
|
[4] |
|
|
|
y en la [2]: |
|
|
| H = |
|
vo² sen² α |
- |
5 m/s² . vo² sen² α |
|
|
|
| 10 m/s² |
(10 m/s²)² |
|
|
|
| Dejame que la simplifique un poco antes de seguir: |
|
|
| |
| H = |
|
vo² sen² α |
|
|
| 2 . 10 m/s² |
|
[5] |
|
|
|
| De la [4] despejo vo²: |
|
|
| vo² = |
|
D . 10 m/s² |
|
|
| sen α . cos α |
|
|
|
| y lo meto en la [5]. |
|
|
| H = |
|
D . sen² α |
|
|
| 2 . sen α . cos α |
|
|
|
|
|
|
H = ½ D . tg α
|
|
|
| |
tg α = 2H / D |
respuesta a) |
|
|
|
Fijate lo siguiente... si ya tenés suficiente entrenamiento en tiros oblicuos y alguna experiencia en geometría y trigonometría, coincidirás conmigo en que la propuesta a) era la única posible. Para llegar a esa conclusión basta con que mires el triángulo formado por el punto de partida y el muro. La tangente del ángulo agudo inferior vale H/D... y el ángulo de disparo, α, es mayor que éste... la unica posibilidad es la respuesta correcta. |
|
|
*Este ejercicio fue tomado en el examen final de Física de julio de 2011.
Para ver el tema de examen completo hacer click acá. |
|
|
DESAFIO: Si el proyectil llega al piso, ¿a qué distancia del muro pega? |
|
 |
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. También se permite que sea sin reproducción... ¿se comprende? Última actualización mar-13. Buenos Aires, Argentina. |
|
|
| |
|

