 |
NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA
(Tiro oblicuo)
|
|

|
| NMS c5.27 - Desde la base de un plano inclinado un ángulo de 9 grados se arroja hacia arriba un proyectil, con un ángulos de 37 grados respecto a la horizontal y una velocidad de 6 metros por segundo. Hallar en qué posición el proyectil impacta sobre el plano. |
|
Este ejercicio es un clásico de cursos de física avanzados, rara vez lo encontramos en cursos iniciales. Los libros que lo tienen lo resuelven con estrategia (después te cuento cuál), yo lo incorporé para mostrarte que el método que yo propongo es infalible, y que hace de este ejercicio "avanzado" un simple ejercicio más.
Como cualquier ejercicio de cinemática, arrancamos con un esquema: |
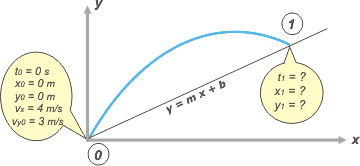 |
Acordate que:
vx = vo cos 37°
voy = vo sen 37°
Y que si elegimos un SR que apunta hacia arriba la gravedad es negativa. |
|
|
|
¿Cuántas ecuaciones horarias describen el movimiento? Tres, porsupu, como todo TO. Para hallarlas basta con reemplazar las constantes (to , xo , yo , vx , voy , y g) de las ecuaciones generales de los tiros oblicuos:
x = xo + vx ( t – to )
y = yo + voy ( t – to ) + ½ g ( t – to )²
vy = voy+ g ( t – to )
En el esquema, en el globito que habla del punto 0, están todas las constantes que necesitamos para armar las ecuaciones que describen el movimiento del cuerpo.
x = 4 m/s . t
y = 3 m/s . t – 5 m/s² . t²
vy = 3 m/s – 10 m/s² . t
|
|
|
La última ecuación, la de velocidad no vamos a necesitarla. Pero aún falta una cuestión muy importante: la posición del impacto debe estar sobre el plano, sin esa condición no tenemos forma de encontrarla. En el plano x-y todos los puntos pertenecen a una recta cuya ecuación será del tipo y = mx + b (como consigné en el esquema), donde b es la ordenada al origen (que vale 0) y m es la pendiente que no es otra que la tangente de 9 grados (0,16). O sea:
y = 0,16 . x
Lo que resta ahora es muy sencillo; basta con que les pidamos a las ecuaciones que hablen del punto de interés, el 1. |
|
|
 |
x1 = 4 m/s . t1 |
|
[1] |
| y1 = 3 m/s . t1 – 5 m/s² . t1² |
|
[2] |
| y1 = 0,16 . x1 |
|
[3] |
|
|
Estas son las ecuaciones especializadas para los instantes que a vos te interesan. |
Me lo temía: quedó un sistema de tantas ecuaciones como incógnitas (3x3), en las que las incógnitas, si sabemos interpretarlas, son las que nos pide el enunciado del problema. Quiere decir que acá terminó la física del problema... lo que resta es álgebra. Y es bastante sencilla.
Reemplazo la ecuación [1] y [2] en la [3]:
3 m/s . t1 – 5 m/s² . t1² = 0,16 . 4 m/s . t1
Igualo a 0 y hallo t1
0 = – 2,36 . 4 m/s . t1 + 5 m/s² . t1²
0 = – 2,36 m/s + 5 m/s² . t1
t1 = 0,47 s
Con ese valor vuelvo a las ecuaciones [1] y [2] para hallar x1 e y1. |
|
|
|
|
|
La estrategia común de resolución de este ejercicio consiste en resolver la intersección de dos curvas: una recta (que representa al plano) y una parábola (que representa la trayectoria del proyectil y que surge de la ecuación de la trayectoria). |
|
|
DESAFIO: Averiguar si el impacto se produce con el proyectil aún subiendo o ya bajando (como representé en el esquema). |
|
 |
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. También se permite que sea sin reproducción... ¿se comprende? Última actualización feb-13. Buenos Aires, Argentina. |
|
|
| |
|

