NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA
(Tiro oblicuo)
|
|

|
| NMS c5.23*- Un avión que vuela horizontalmente a 1.200 metros de altura con una velocidad de 200 km/h deja caer una bomba sobre un blanco situado en tierra. Determinar el ángulo formado por la vertical y la línea que une el avión con el blanco en el instante en que se suelta la bomba. |
|
Acá tenemos un ejercicio bélico. Antes eran más frecuentes, ahora por suerte son casi piezas de museo. Este es de un libro de 1980. Pareciera que los educadores están tomando partido por los ejemplos de la paz. Me alegro.
La clave del asunto, el lugar de interpretación más peligroso, pasa por comprender que la velocidad inicial de la bomba es la misma que la del avión, o sea, una velocidad horizontal de 200 km/h, y de paso la pasamos a metros por segundo para unificar las unidades. 200 km/h = 55 m/s
Ahora que está aclarado el asunto empecemos, como siempre, por el esquema. |
|
|
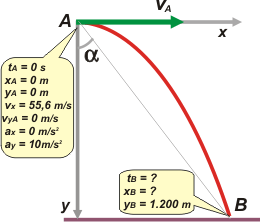 |
Nos interesan sólo dos eventos: cuando se suelta la bomba desde el avión, A; y cuando llega al blanco, B.
Teniendo los modelos de ecuaciones horarias para los tiros oblicuos a la vista, reemplazamos las constantes por las constantes que figuran en el globito de A.
x = 55,6 m/s . t
y = 5 m/s² . t²
vy = 10 m/s² . t
Habrás notado que elegí un sistema de referencia positivo hacia abajo. De vez en cuando hay que variar. |
| |
En general
No me salen
utiliza el valor aproximado de g = 10 m/s² |
|
La tercera ecuación no aporta nada en este ejercicio, ya que nada nos dicen ni nos preguntan acerca de la velocidad de la bomba durante la caída. A las otras dos, les vamos a pedir que hablen del momento B. |
|
|
| |
xB = 55,6 m/s . tB |
[1] |
| |
1.200 m = 5 m/s² . tB² |
[2] |
|
|
Estas son las ecuaciones especializadas para el instante que a vos te interesa. |
Tenemos un sistema de 2x2... o sea, con solución algebraica... y podremos decir cuánto vale tB y xB.
Me imagino que querrás que yo lo haga. De la [2] despejo tB.
tB² = 1.200 m / 5 m/s²
tB= 15,5 s
eso lo meto en la [1]. y calculo xB
xB = 55,6 m/s . 15,5 s
xB = 862 m
El ángulo que nos piden, α, lo hallamos haciendo un poco de trigonometría. Te habrás dado cuenta que entre la vertical, el desplazamiento horizontal medido sobre el piso, y la recta que une al avión con el blanco se forma un triángulo rectángulo, de modo que:
tg α = xB / yB =
tg α = 862 m / 1.200 m =
tg α = 0,72
de donde: |
|
|
|
|
|
| Supuestamente el artillero, conociendo la velocidad del avión y la altura a la que vuela, hace este cálculo para saber dónde y cuándo dejar caer la bomba. Pero la verdad era otra, ya que para estas alturas la resistencia del aire hace que la caída no sea parabólica y a los 4 o 5 segundos de caída el movimiento ya es casi vertical. |
|
|
| |
|
 |
*Este ejercicio fue tomado y adaptado de Física general, Carel W. van der Merwe, Editorial Mc Graw-Hill, Naucalpan de Juárez, México, 1980.
|
|
| Desafío: ¿Con qué velocidad llega la bomba al blanco? |
|
| Algunos derechos reservados.
Si en el básquet quieres encestar, no pierdas tiempo en plantear ecuaciones, sólo usa tu intuición y habilidad. Se permite su reproducción citando la fuente. Última actualización may-12. Buenos Aires, Argentina. |
|
|
| |
| |
|

