Cualquiera lo sabe, en especial los lanzadores de jabalina o de martillo, o de piedras o de cualquier porquería. El ángulo que mayor alcance le da a un tiro oblicuo es el de 45º. Te lo voy a tratar de demostrar.

Partamos de las ecuaciones horarias de posición para el TO.

x = x_o + v_x ( t – t_o )

y = y_o + v_oy ( t – t_o ) + ½ g ( t – t_o )²

Para hacer las cosas más sencillas tomemos t_o = 0 s y x_o = y_o = 0 m, con un SR vertical hacia arriba; mirá el esquema:

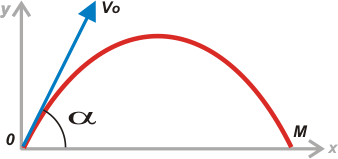
Entonces las ecuaciones quedan así:

x = v_x . t

y = v_oy . t – ½ g . t²

recordemos que

v_x = v_o cos α

v_oy = v_o sen α

Llamemos x_M al alcance que, como ya te diste cuenta, se alcanza (valga la redundancia) en un punto que llamamos M, en una altura y_M = 0 m

x_M = v_o cos α . t_M

0 m = v_o sen α . t_M – ½ g . t_M²

de la segunda ecuación despejo t_M

t_M = 2 v_o sen α /g

Eso lo meto en la de x_M...

x_M = v_o cos α . t_M

x_M = v_o cos α (2 v_o sen α /g)

x_M = 2 v_o² cos α sen α /g

Ya estamos llegando, tené paciencia. Hay una relación trigonométrica que podés buscar en cualquier libro de matemática o en internet y que yo no te voy a demostrar pero que si vos querés podés poner a prueba con tu calculadora. Es ésta:

2 . sen α . cos α = sen (2 α)

A eso justamente se refería el enunciado, ¿te acordás? Por último, entonces, la expresión para el alcance queda así... y después la analizamos:

x_M = v_o² sen (2 α) / g

Qué nos dice esta expresión. Por un lado, que el alcance va a ser tanto mayor cuanto mayor sea la velocidad inicial del disparo...: chocolate por la noticia. Pero mirá que dice algo que vos no sabías... que el alcance es proporcional al cuadrado de la velocidad, o sea, depende fuertemente de ella. Otra cosa que dice es que es inversamente proporcional a la gravedad, o sea que en un planeta con mayor gravedad las cosas que tirás no llegan tan lejos, y en la Luna tenés que tener más cuidado porque tirás algo y después ir a buscarlo te cuesta un fangote de viáticos.

Pero lo que nos interesa viene ahora. El alcance es directamente proporcional al seno de (2α). La función seno varía entre 1 y –1, y alcanza el valor máximo, 1, cuando el argumento (en este caso 2α) vale 90° . De modo que si

2α = 90°

Según aprendí en el libro de Miguel Hoyuelos, los atletas lanzadores lo hacen con ángulos de entre 40 y 42 grados (un poco menores que los de alcance máximo).
Los motivos son dos: el punto de llegada está más abajo del de partida, y el cuerpo humano arroja con más fuerza hacia adelante que hacia arriba.

Todavía podemos sacarle un poquito más de provecho a tanto laburo de álgebra. Fijate: dos ángulos que suman 90°, por ejemplo 27° y 63° (los acabo de inventar), sus duplos, 54° y 126°, tienen el mismo valor de seno (corroboralo con tu calculadora). La generalización de esto sería:

Si (α + β) = 90° entonces sen (2α) = sen (2β)

Lo cual significa que si lanzás con 27° o con 63° da lo mismo, obtenés el mismo alcance. Y lo mismo con cualquier par de ángulos que sumen 90°. Bueno, no se me ocurre nada más. Terminamos.

DESAFIO: Que con dos ángulos diferentes obtengas el mismo alcance no quiere decir que tarden lo mismo... Hallar una expresión para la diferencia de tiempo en la tardanza de dos disparos con ángulos de igual alcance. (Sólo para genios de la talla de Einstein o Maradona).