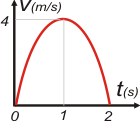
No es sencillo, pero tampoco imposible. No desesperes.

La clave del ejercicio figura en una palabra del enunciado: parábola. El razonamiento es el siguiente: si la velocidad varía de tal modo que su gráfica es una parábola, varía cuadráticammente, y la aceleración (que es la magnitud que describe cómo varía la velocidad) debe variar linealmente, y su gráfica debe ser una recta oblicua.

Es lo mismo que ocurría en el MRUV con la posición y la velocidad: si la posición variaba de tal forma que su gráfica era una parábola, la velocidad se graficaba con una recta oblicua.

Dicho matemáticamente: si la velocidad es una función de segundo grado, la aceleración debe ser una función de primer grado. Tal vez se te aclare el panorama recordando que la aceleración es la derivada de la velocidad. Si te olvidaste las reglas de la derivación podés encontrarlas acá.

Siguiendo con nuestro razonamiento, la función que describe la variación de la aceleración, llamada tirón, j, debe ser constante (y su gráfica debe ser una recta horizontal).

Estos movimientos en los que la velocidad varía con el cuadrado del tiempo (o la aceleración varía uniformemente) se llaman movimientos de tirón constante y, lógicamente, pertenecen al grupo de los movimientos con aceleración dependiente del tiempo. Los modelos de ecuación horaria de estos movimientos los tenés acá (para simplificar muestro el caso particular en el que t₀ = 0 s):

x = x₀ + v₀ t + (1/2) a₀ t² + (1/6) j t³

v = v₀ + a₀ t + (1/2) j t²

a = a₀ + j t

j = cte

Aunque nunca hallas visto estos modelos (ni los tengas en tu hoja de fórmulas) se puede llegar a ellos fácilmente si recordás los principios básicos de la derivación y la integración.

Pero además, fijate que la ecuación de posición no nos interesa para nada ya que el enunciado nada dice ni pregunta sobre las posiciones de la partícula. La única ecuación que nos interesa es la de velocidad:

v = v₀ + a₀ t + ½ j t²

Luego, procedemos de la misma manera que lo hicimos con todos los ejercicios de cinemática siempre: le pedimos a esa ecuación que hable de los instantes que nos interesan. En el gráfico están esos datos: en el instane inicial v₀ = 0, en el instante 1 s la velocidad vale 4 m/s y en el instante 2 s la velocidad se anula.

4 m/s = a₀ 1 s + ½ j 1 s²

0 m/s = a₀ 2 s + ½ j 4 s²

Con lo cual llegamos a un sistema de 2 ecuaciones con 2 incógnitas, donde las incógnias son a₀ y j.

Despejemos j de la segunda:

j = — a₀ / s

Y eso lo metemos en la primera:

4 m/s = a₀ s — ½ a₀ s

4 m/s = ½ a₀ s

Ya llegamos:

Ya que estamos calculemos el tirón (tanto en la primera como en la segunda ecuación deben dar el mismo resultado:

j = — 8 m/s³

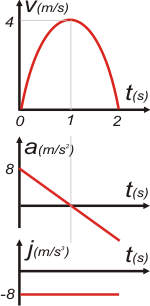
Y es lo que ocurre.

No podemos irnos sin hacer los gráficos y disfrutar de ellos.