NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Movimiento uniformemente variado)
|
|

|
 |
NMS c3.48- Se dispara un objeto verticalmente hacia
arriba, con una velocidad de 30 m/s. Se pide: |
| a - |
Elegir un sistema de referencia, que mantendrá
invariable en todo el desarrollo, y plantear
las ecuaciones horarias del movimiento. Justificar
los valores y signos asignados. |
| b - |
Calcular su posición y velocidad al cabo de
2 s; 4 s; y 8 s de su lanzamiento. Hallar los desplazamientos
entre 0 y 2 segundos; 2 s y 4 s; 4 s
y 8 s. Interpretar. |
| c - |
Determinar en qué instante vuelve a pasar
por el punto de partida. |
| d - |
Determinar el instante para el que su altura
es máxima, y el valor de dicha altura. |
| e - |
Hallar en qué instante se encuentra a 25 m
de altura. |
| f - |
Graficar la altura alcanzada, la velocidad y la
aceleración del objeto, en función del tiempo. |
|
¿Nada más?, OK, nos preparamos unos matecitos amargos (no existe otro tipo de mate)... Y esta vez no voy a hacer un esquema. El motivo es que nos piden tantas cosas... tantas... que el esquema quedaría un mamarracho. Además hay muchas situaciones sobre las que nos habla el enunciado que no podemos predecir dónde localizarlas y lo más probable es que las situemos en lugares que no se correspondan con las correctas. (Eso no es nada grave, y es bastante común; el esquema aún así -errado- sigue siendo útil). Pero temo confundirte. En cambio, voy a aprovechar este ejercicio para machacarte la fecunda e importantísima idea de la ecuación horaria.
Si tenés los modelos de ecuación horaria de tiro vertical a mano:
y = yo + vo ( t – to ) + ½ g ( t – to )²
v = vo + g ( t – to )
y reemplazás las constantes iniciales (que te dibujé en azul y que son decisiones tuyas)... nos quedan las ecuaciones horarias que describen todo el movimiento de nuestro objeto... y responden todas las preguntas del ejercicio. Tomemos el punto de partida como nivel cero (yo= 0m), que arranca en el instante cero (to= 0s) con un sistema de referencia, SR, que apunta hacia arriba (g = – 10 m/s²). Hecho todo esto las ecuaciones horarias quedan así:
| | |
y = 30 m/s . t – 5 m/s² . t²
v = 30 m/s – 10 m/s² . t
Ahora podés preguntarles a las ecuaciones lo que quieras... ellas van a responder dócil y amablemente todas las preguntas que les hagas. Por ejemplo: querés saber cuáles son su altura y velocidad en el instante 2s... bien, donde dice t, colocá 2s... luego hacé la cuentita, y del otro lado del igual las ecuaciones te responderán cuánto valen esa altura, y2s, y esa velocidad, v2s. |
|
|
y2s = 30 m/s . 2s – 5 m/s² . 4s² = 60 m – 20 m
v2s = 30 m/s – 10 m/s² . 2s = 30 m/s – 20 m/s
|
|
Fijate que nunca me olvido del subíndice si me estoy refiriendo a un dato en particular. |
|
|
|
Ahora se te antoja saber cuáles eran las posiciones y velocidades en el instante 4s... procedés igual... las ecuaciones horarias nunca se cansan, siempre responden:
y4s = 30 m/s . 4s – 5 m/s² . 16 s²
v4s = 30 m/s – 10 m/s² . 4s
|
|
Subíndices para la posición y la velocidad. No son variables; son las que tiene en ese instante y sólo en ese instante. |
| |
y4s = 40 m; v4s = – 10 m/s |
|
|
|
|
Viste que a los dos y a los cuatro segundos el objeto parece hallarse a la misma altura... tiene su lógica: todo lo que sube, baja. Vos confiá en las ecuaciones horarias... son unas ídolas. Preguntemos por el instante 8s...
y8s = 30 m/s . 8s – 5 m/s² . 64s²
v8s = 30 m/s – 10 m/s² . 8s
|
|
Si no les pusiese subíndice serían variables. Y eso es ridículo: en el instante 8s la posición es una sola... y no cambia. |
| |
y8s = – 80 m; v8s = – 50 m/s |
|
|
|
|
| Ahora los plomos estos quieren que encontremos los desplazamientos entre esas posiciones que acabamos de encontrar... suponen que van a sorprendernos... Démosles el gusto: |
|
|
| |
Δy02 = 40 m; Δy24 = 0 m; Δy48 = – 120 m |
|
|
|
|
Las ecuaciones horarias son tan dúctiles que podés interrogarlas de la manera inversa: en lugar de preguntarles por una posición para un instante les preguntás en qué instante tal posición. Lo único que hay que tocar son las variables... no apretes ningún otro botón, porque cambiás la ecuación y pasa a describir otro movimiento -no el tuyo-; fijate. Te vuelvo a copiar las ecuaciones:
y = 30 m/s . t – 5 m/s² . t²
v = 30 m/s – 10 m/s² . t
Ahora queremos conocer el instante para la posición 0m... bien: donde dice y (en la primera ecuación) ponemos 0m... y la ecuación responde.
0m = 30 m/s . t0m – 5 m/s² . t0m²
Es una cuadrática incompleta, de modo que vamos a obtener dos respuestas. No es que la ecuación sea salame. Es que no tenemos otra forma de preguntarle. Si no te animás a obtener la respuesta solo, yo te ayudo. Saco factor común t0m.
0m = t0m . (30 m/s – 5 m/s² . t0m)
Si el primer factor es cero, obtenemos la respuesta tonta: t0m = 0. Si el segundo factor es el nulo, obtenemos la respuesta interesante:
0m = 30 m/s – 5 m/s² . t0m
t0m = 30 m/s / 5 m/s²
|
|
¡Subíndices! Sólo t0m se corresponde con 0m.
|
| |
|
|
Y ya que estamos preguntémosle a la segunda ecuación qué velocidad tenía el objeto en ese instante.
v0m = 30 m/s – 10 m/s² . 6s
|
|
|
|
|
|
Ahora vamos a preguntarle por la altura máxima del vuelo. Voy a llamar a ese instante M, ¿te parece? Fijate cómo pregunto:
yM = 30 m/s . tM – 5 m/s² . tM²
vM = 30 m/s – 10 m/s² . tM
Para encontrar el instante buscado tenés que saber que en ese instante vM = 0 m/s. Si no... fuiste. Acá, las dos ecuaciones deben trabajar juntas. De la segunda despejamos tM, y lo que da lo metemos en la primera:
0 m/s = 30 m/s – 10 m/s² . tM
tM = 30 m/s / 10 m/s² = 3s
yM = 30 m/s . 3s – 5 m/s² . 9s²
|
|
Subíndices |
| |
|
|
La última es la pregunta más difícil, pero a esta altura ya te diste cuenta de que la cinemática es una papa... todo el secreto está en armar correctamente las ecuaciones horarias, y amasijarlas a preguntas. Si querés saber en qué instante el objeto pasó por la posición 25m, bueno... donde dice y tendrás que escribir 25m y despejar el instante de tiempo correspondiente, que no será otro que t25m.
25 m = 30 m/s . t25m – 5 m/s² . t25m²
Es una cuadrática completa. Hay que ordenarla, y usar la formulita de los griegos.
0 = – 25 m + 30 m/s . t25m – 5 m/s² . t25m²
Se obtienen dos valores posibles. En este caso los dos son útiles |
|
Subíndices |
|
|
|
Y ya que estamos le pedimos a la segunda ecuación que nos cuente qué velocidades tenía el móvil en esos instantes.
v25m = 30 m/s – 10 m/s² . 1s
v'25m = 30 m/s – 10 m/s² . 5s
|
|
|
| |
v25m = 20 m/s ; v'25m = – 20 m/s |
|
|
|
|
|
|
|
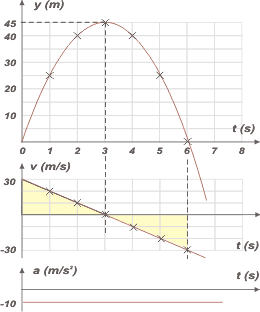 |
Ya que nos gastamos tanto en resolver este ejercicio... los gráficos serán cuantitativos.
Como siempre, en tándem, o sea, con una misma escala de tiempo, encolumnados en el orden preciso de posición-velocidad-aceleración. Apreciá cómo se corresponden entre sí (por ejemplo velocidad nula con el vértice de la parábola, donde su inclinación es nula).
Mirá las áreas sombreadas, calculalas. Puse crucecitas en los instantes calculados.
La posición en el instante 8s te la debo, porque se me iba mucho de escala. |
|
|
|
| |
|
 |
| Desafío: tenés que rehacer todo, pero ahora con un SR idéntico, salvo en que el instante de la partida vale 30 s. |
|
 |
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Última actualización may-08. Buenos Aires, Argentina. |
|
|
| |
| |
|

