 |
NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Movimiento uniformemente variado)
|
|

|
 |
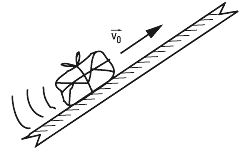
NMS c3.46- Se lanza un paquete hacia arriba, con
una velocidad de 3 m/s, por un tablón inclinado
con rozamiento no despreciable. El paquete sube
en línea recta hasta detenerse, y regresa luego al
punto de partida. Asciende durante 2 segundos,
y desciende durante 4 segundos. |
a - Hallar la aceleración que actúa en el ascenso,
y la distancia que recorre sobre el plano, hasta
detenerse.
b - Hallar con qué aceleración desciende, y la
velocidad con que llega al lugar de partida.
c - Trazar los gráficos de aceleración, velocidad
y posición del paquete, en función del tiempo. |
 |
|
Tal vez, lo primero que desconcierta de este ejercicio es que la trayectoria está inclinada. No tenés que hacerte problema por eso... alcanza con que apoyes sobre ese plano inclinado una regla lo suficientemente larga y listo: la usás como sistema de referencia. El esquema -a gusto tuyo- podés hacerlo inclinado u horizontal.
| | |
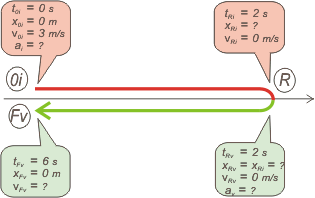 |
Pero hacelo, porque es fundamental. Si no lo hacés... fuiste.
Te dibujé en rojo la ida y en verde la vuelta. Son dos movimientos diferentes. Son ambos MRUV, pero tienen aceleración diferente. Llamé R -por retorno- al final del viaje de ida e inicio del viaje de vuelta.
El enunciado no lo dice, pero regresa al punto de partida. |
|
|
|
| Si hiciste bien el esquema, armar las ecuaciones horarias es un juego de niños. Las constantes del movimiento de ida las tenés en el primer globito rosa, que describe el inicio de ese movimiento, 0i. Y las constantes para armar las ecuaciones de vuelta las tenés en el globito verde del punto de retorno, R. Fijate cómo quedan. |
|
|
| ida |
x = 3 m/s t + ½ ai t² |
|
Estas son las ecuaciones que describen TODO el movimiento de ambos móviles. No hablan sólo de las situaciones que a vos te interesan, hablan de los infinitos instantes que transcurren durante el movimiento. |
| |
v = 3 m/s + ai t |
|
| vuelta |
x = xR + ½ av ( t – 2s)² |
|
| |
v = av (t — 2s) |
|
Donde ai y av son las aceleraciones de ida y vuelta, respectivamente.
Ahora que tenemos las herramientas que describen todo el movimiento... las usamos: les pedimos que hablen de los puntos interesantes... aquellos donde hay datos o incógnitas, por ejemplo R, F... |
 |
xR = 3 m/s 2s + ½ ai (2s)² |
[1] |
(ec. de ida habla de R) |
| 0 m/s = 3 m/s + ai 2s |
[2] |
(ec. de ida habla de R) |
| 0 m = xR + ½ av (4s)² |
[3] |
(ec. de vuelta habla de F) |
| vF = av 4s |
[4] |
(ec. de vuelta habla de F) |
|
|
|
Me lo temía... desembocamos sin quererlo en un sistema de tantas ecuaciones como incógnitas (4x4), esto tiene solución. Eso quiere decir que acá terminó la física, y lo que viene es álgebra... qué porquería. Pero bueno, una vez más se ve que el método es infalible.
De la [2] despejo ai y la calculo.
ai = — 3 m/s / 2s
|
|
 |
| |
|
|
Ahora voy con este valor a la [1] y calculo xR
xR = 3 m/s 2s — 0,75 m/s² 4 s²
|
|
Este ejercicio ya es un paquete. |
|
|
|
Ahora voy con este valor a la [3] y calculo av (qué aburrido es todo esto...)
0 m = 3 m + ½ av 16 s²
|
|
|
|
|
|
|
|
|
Es negativa, ¿qué signfica esto? Si mirás atentamente el SR, te das cuenta de que cuando baja ¡lo hace cada vez más rápido! Por último voy a la [4] y calculo la velocidad final del viaje de regreso.
vF = — 0,37 m/s² . 4 s
|
|
Paquete
total. |
|
|
|
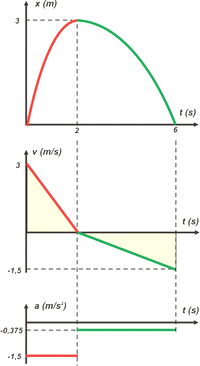
| Si hay una lección importante en este ejercicio es: ¡qué herramienta enorme es el esquema! Ahora analicemos los gráficos. |
|
|
|
Te voy a tratar de hacer una descripción acabada de todo lo que puede verse en estos gráficos.
Lo primero es el formato tándem: encolumnados en el orden posición-velocidad-aceleración y con una misma escala de tiempo.
Ahora mirá el de posición: se trata de dos parábolas, ambas de concavidad negativa, la primera más cerrada, la segunda más abierta. En el instante 2s ambas tienen una inclinación nula (una tangente igual a cero). La roja está más inclinada en 0s que la verde en 6s.
Vamos al de velocidad: se trata de dos rectas de función descendente. La roja, de mayor pendiente que la verde. Las áreas encerradas "debajo" de las respectivas curvas son iguales (si tenés dudas hacé las cuentas, es fácil, son dos triángulos). Ambas rectas están en la velocidad 0 en el instante 2s.
Por último el de aceleración: dos rectas horizontales bajo el eje de los tiempos. En el instante 2s salta de un valor a otro. Todo bien. |
|
|
|
| DESAFIO: Tratá de resolver esto: ¿en qué instantes y con qué velocidades pasa el paquete por la posición 1,2 m? |
|
 |
Algunos derechos reservados.
Se permite su reproducción citando la fuente. Última actualización may-08. Buenos Aires, Argentina.
|
|
| | | |
|

