|
NO ME SALEN
SOLVED PROBLEMS IN PHYSICS
Accelerated Motion, (AM)
|
|

|
 |
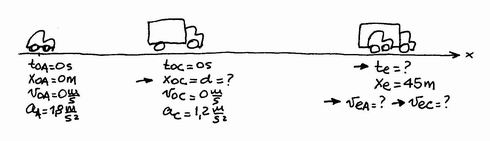
3.43 - A car and a truck start simultaneously, from rest, with the car at some distance behind the truck. Both of them are moving with constant acceleration, 1,8 m/s² for the car and 1,2 m/s² for the truck, and they cross over when the car is at 45 meters from its departure spot. Find: |
|
a) How much time did the car take to get at the truck
b)Initially, what was the distance between them
c) The speed of each vehicle when they are along
d) The position and speed graphs vs time, for both of them
First of all, as usual, we start with the sketch. |
 |
|
Así eran los esquemas de No Me Salen cujando los hacía a manopla... simpáticos, ¿no? |
Now we ask ourselves ¿How many equations describe this problem? Exactly four. Since here we have two uniformly varied movements, and each AM is described by two equations: |
|
|
 |
x = xo + vo ( t – to ) + ½ a ( t – to )2
v= vo + a ( t – to ) |
|
|
This are the "regular", for every AM To find the ones in our problem we will have to replace the equations´s constants (to, xo, vo y a) for the "initials" of each movement. |
|
|
| car |
x = 0,9 m/s² . t²
v = 1,8 m/s² . t |
|
Estas son las ecuaciones que describen TODO el fenómeno del movimiento que narra el enunciado. |
| truck |
x = d + 0,6 m/s² . t²
v = 1,2 m/s² . t |
|
Since the tools are arranged on the table (the time formulas), now we use them. They will solve our problem. Let´s ask them to "talk" about the encounter. They say then: |
|
|
 |
|
| 45 m = 0,9 m/s² . te² |
[1] |
| vAe = 1,8 m/s² . te |
[2] |
| 45 m = d + 0,6 m/s² . te² |
[3] |
| vCe = 1,2 m/s² . te |
[4] |
|
Estas, en cambio, son las ecuaciones especializadas para los instantes que a vos te interesan. |
If all went well, the problem must be solved, let´s see?...Yes, exactly, is written above a system with many equations as unknowns (4x4). In it, the unknowns are the ones that the problem ask for.
But really the problem ends here? Here ends the physics of the problem. The rest is algebra and is not so dramatic. The system is simple. If we look the first equation, it has one unknown; starting from there, everything turns out much easier. |
|
|
| |
|
|
| With that I´ll go to the third one [3] and comes d |
|
|
|
|
|
| And finally, to the two that are missing, from where come the encounter´s speeds |
|
|
| |
|
|
|
|
|
Ultimately, the graphs. Look how I do them: columned, always in the same order, and with the same time scale; some people call this manner "in tandem". |
|
|
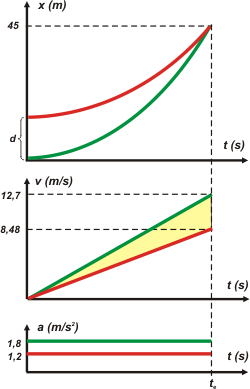 |
The graphs always look like four crazy lines...but they are full of information, full of technic...
Look, for example, the kind of curve of the position´s graphs. They are arcs of parable that start at the initial time with zero slope (horizontal). When they cross, they have different slopes (it couldn´t be other way). They have positive concavity (smiling). They start displaced, a segment representing the distance between the mobiles. And I could go on describing some more...
The speed curves are straight segments and start from the zero position. They have positive slope. They drift apart...
Do you dare to tell me how much is the area that I marked you in yellow, without accounts? Well, if you don´t...do it anyway. |
|
|
|
| And to all this you have to add the temporal correspondence of the three graphics (the powerfull idea of tandem). Do you dare to remake the graphs for the same problem, proposing from a RS with opposite direction of the movement? |
|
|
| CHALLENGE: Remake all the problem but knowing that the truck starts 2s later than the car. |
|
 |
| Translated by Florencia Torres . Some Rights Reserved. Not allowed to be copied without naming either the author or this source material. Last Updated March-14. Buenos Aires, Argentina. |
|
|
| |
|