 |
NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Movimiento uniformemente variado)
|
|

|
 |
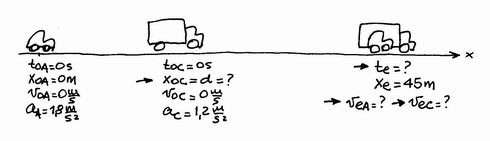
NMS c3.43 - Un automóvil y un camión parten simultáneamente, desde el reposo, con el auto a cierta distancia detrás del camión. Ambos se mueven con aceleración constante, de 1,8 m/s² para el automóvil y de 1,2 m/s² para el camión, y se cruzan cuando el auto se halla a 45 m de su lugar de partida. Hallar: |
|
a - Cuánto tiempo tardó el auto en alcanzar al camión.
b - Qué distancia los separaba inicialmente.
c - La velocidad de cada vehículo cuando están a la par.
d - Los gráficos de posición y velocidad en función del tiempo, para ambos.
Como ya es costumbre (aunque no lo hacemos por costumbre) comenzamos con un esquema. |
 |
|
Así eran los esquemas de No Me Salen cujando los hacía a manopla... simpáticos, ¿no? |
Ahora nos preguntamos, ¿cuántas ecuaciones describen este problema? Exactamente, cuatro. Ya que acá tenemos dos movimientos uniformemente variados, y cada M.R.U.V. se describe con dos ecuaciones del tipo: |
|
|
 |
x = xo + vo ( t – to ) + ½ a ( t – to )2
v= vo + a ( t – to ) |
|
|
Estas son las "generales", para todo M.R.U.V. Para hallar las de nuestro problema habrá que reemplazar las constantes de las ecuaciones (to, xo, vo y a) por las "iniciales" de cada movimiento. |
|
|
| auto |
x = 0,9 m/s² . t²
v = 1,8 m/s² . t |
|
Estas son las ecuaciones que describen TODO el fenómeno del movimiento que narra el enunciado. |
| camión |
x = d + 0,6 m/s² . t²
v = 1,2 m/s² . t |
|
Ya están las herramientas dispuestas sobre la mesa (las ecuaciones horarias), ahora las usamos. Ellas solitas nos resolverán el problema. Pidámosles que "hablen" del encuentro. Ellas dicen entonces: |
|
|
 |
|
| 45 m = 0,9 m/s² . te² |
[1] |
| vAe = 1,8 m/s² . te |
[2] |
| 45 m = d + 0,6 m/s² . te² |
[3] |
| vCe = 1,2 m/s² . te |
[4] |
|
Estas, en cambio, son las ecuaciones especializadas para los instantes que a vos te interesan. |
Si todo anduvo bien, el problema ya tiene que estar resuelto, ¿a ver?... Sí, efectivamente, arriba hay escrito un sistema de tantas ecuaciones como incógnitas (4x4), en el que las incógnitas son las que nos pide el enunciado del problema.
¿Pero realmente aquí termina el problema? Aquí termina la física del problema. El resto es álgebra y no es tan dramático. El sistema es sencillo. Si miramos la primera ecuación, ella tiene una sola incógnita; empezando por ahí, resulta todo muy fácil. |
|
|
| |
|
|
| con eso voy a la tercera, [3] y sale d |
|
|
|
|
|
| y por último a las dos que faltan, de donde salen las velocidades en el encuentro |
|
|
| |
|
|
|
|
|
Por último los gráficos. Fijate cómo los hago: encolumnados, siempre en el mismo orden, y con una misma escala de tiempo; algunos llaman a esta manera "en tándem". |
|
|
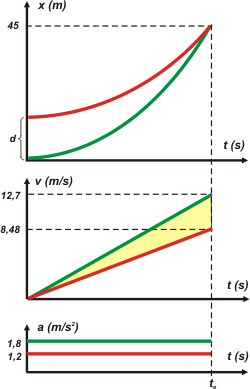 |
Los gráficos siempre parecen cuatro líneas locas... pero están llenas de información, llenas de técnica...
Mirá por ejemplo el tipo de curva de las gráficas de posición. Son arcos de parábola que arrancan en el instante inicial con una inclinación nula (horizontales). Cuando se cruzan tienen inclinaciones diferentes (no podría ser de otra manera). Tienen concavidad positiva (sonriente). Arrancan desplazadas un segmento que representa la distancia de separación de los móviles... Y así podría seguir describiendo un rato más...
Las curvas de velocidad son segmentos rectos. Arrancan de la posición cero. Tienen inclinación positiva. Se van separando...
¿A que no te animás a decirme cuánto vale el área que te marqué en amarillo, sin hacer cuentas? Bueno, si no te animás... hacelo igual. |
|
|
|
| Y a todo esto tenés que sumarle la correspondencia temporal de la terna de gráficos (la poderosa idea del tándem). ¿Te animarías a rehacer los gráficos para este mismo problema, planteado desde un SR de sentido contrario al de los movimientos? |
|
|
| DESAFIO:
Rehacer todo el problema pero sabiendo que el camión arranca 2 s después que el auto. |
|
 |
| Algunos derechos reservados.
Se permite su reproducción citando la fuente (se aclara que por "fuente" se entiende al autor y al sitio, www.neuro.qi.fcen.uba.ar/ricuti, no a la fuente de Trevi ni a ninguna otra que largue agua). Última actualización jun-08. Buenos Aires, Argentina. |
|
|
| |
|

