NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Movimiento uniformemente variado)
|
|

|
 |
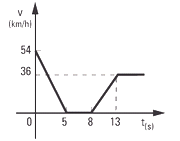
NMS c3.40 - El gráfico dado representa la velocidad en
función del tiempo, para un automovilista que se
detiene frente a un semáforo y luego arranca.
|
 |
a -Trazar los gráficos correspondientes de aceleración
y de posición en función del tiempo.
b - Hallar a qué distancia del semáforo se encontraba
en el momento en que comenzó a frenar,
si pasó frente a él en el instante t = 10 segundos. |
|
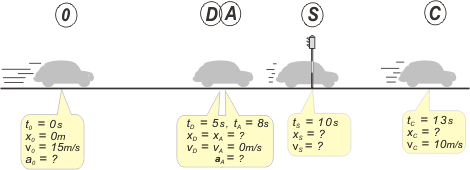
| Vamos a transgredir un poquito y lo resolvemos en el orden no me salen, o sea: dejamos los gráficos para el final y empezamos por un esquema. Conste que no lo hago para que vos entiendas bien el enunciado... lo hago porque es una herramienta casi indispensable, también para que vos aprendas a hacerlos... ¡y para que los hagas siempre! |
|
|
paso 1 |
Como vemos en el gráfico de velocidad, hay dos movimientos variados. Al evento ocurrido 10 segundos antes de pasar al lado del semáforo lo llamé 0, y lo voy a tomar como inicio del primer movimiento, que termina en D (por detención). Se queda en el mismo lugar detenido. A es el nombre que le puse al nuevo arranque; S, cuando se cruza con el semáforo y C, cuando alcanza la velocidad crucero y decide pasear a esa velocidad.
De 0 a D, hay un MRUV y de A a C, otro MRUV. ¿Tenés los modelos de MRUV?
x = xo + vo ( t – to ) + ½ a ( t – to )²
v = vo + a ( t – to )
Para reemplazar las constantes en los modelos, lo más práctico es usar las que tenés en los globitos de los inicios de cada movimiento: 0 para la frenada, A para el arranque. |
|
|
| x, 0D |
x = 15 m/s . t + ½ ao . t²
|
|
| v, 0D |
v = 15 m/s + ao . t |
|
| x, AC |
x = xD + ½ aA . ( t – 8 s )²
|
|
| v, AC |
v = aA . ( t – 8 s ) |
|
| Ahora les pedimos a estas ecuaciones que hablen de aquellos eventos de los que puedan decir algo interesante: |
| x, 0D, en D |
xD = 15 m/s . 5 s + ½ ao . 25 s² |
[1] |
| v, 0D, en D |
0 m/s = 15 m/s + ao . 5 s |
[2] |
| x, AC, en S |
xS = xD + ½ aA . ( 10 s – 8 s )² |
[3] |
| v, AC, en C |
10 m/s = aA . ( 13 s – 8 s ) |
[4] |
|
|
paso 2
paso 3 |
No lo vas a poder creer: yo conté, y encontré 4 ecuaciones y 4 incógnitas. Acá se acabó la física y empieza el álgebra. Pero no desesperes, No me salen está de oferta y te resuelve el álgebra de ese sistema. De [2] despejo ao y la calculo.
ao = –15 m/s / 5 s = – 3 m/s²
con este valor voy a [1] y calculo xD.
xD = 15 m/s . 5 s – 1,5 m/s² . 25 s² = 37,5 m
Con la [4] averiguo el valor de aA.
aA = 10 m/s / 5 s = 2 m/s²
con estos dos últimos valores voy a la [3] y sale la posición del semáforo, o sea la distancia que nos pide el enunciado:
xS = 37,5 m + 1 m/s². 4 s²
|
paso 4
paso 5
|
|
|
| Ahora sí, hacemos los gráficos como siempre, encolumnados, en orden y escala. |
|
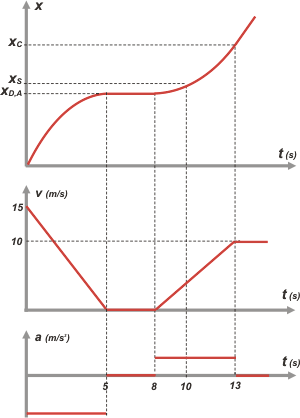 |
Acá tenés un montón de detalles para prestar atención... y aprender a confeccionar gráficos.
Mirá la correspondencia a-v-x para cada tramo de movimiento. Por ejemplo: en el primero la aceleración era constante y negativa... por lo tanto la velocidad es linealmente decreciente y la gráfica de posición un arco de parábola de concavidad negativa. Y así los otros tramos.
Fijate cómo los ceros de velocidad se corresponden con pendientes (inclinaciones) nulas de posición.
Mirá la forma general de las curvas: la de posición debe ser continua y suave (sin puntos angulosos). La de velocidad debe ser continua pero puede tener esquinas. La de aceleración -en cambio- puede tener saltos. |
|
paso 6 |
| |
| DESAFIO: Poné la mano derecha sobre de tu corazón y leé esto en voz alta: "Yo, como cualquier otro mortal de la Tierra, habría armado la ecuación horaria del segundo tramo con un instante de tiempo inicial igual a cero. Ahora me doy cuenta de que el exceso de trabajo por hacer las cosas bien y respetar un SR coherente con un solo instante que valga cero era ínfimo, y valía la pena. ¡Oh! ¡Gracias! Loados sean los No me salen porque con ellos lograré la inmortalidad científica. Amén." |
|
 |
| |
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Última actualización dic-06. Buenos Aires, Argentina. |
|
|
|

