 |
NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Movimiento uniformemente variado)
|
|

|
 |
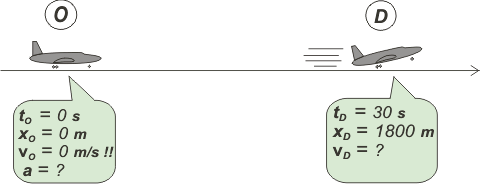
NMS c3.38 - Un avión parte del reposo con aceleración constante y carretea 1800 m por la pista, durante 30 segundos, hasta despegar. ¿Con qué velocidad abandona la pista? Trazar un gráfico velocidad-tiempo. |
|
| Obvio, microbio: lo primero es el esquema. |
|
|
 |
|
|
Ahora escribimos las ecuaciones horarias que describen el movimiento del avión. Porsupu, como todo MRUV. Para hallarlas reemplazamos las constantes de los modelos del MRUV (to, xo, vo y a) por las "iniciales" de nuestro problema.
Estos son los modelos:
x = xo + vo ( t – to ) + ½ a ( t – to )2
v = vo + a ( t – to )
Así quedan después del reemplazo de constantes. Mirá qué bonitas.
x = ½ a t 2
v = a . t
Ahora les pedimos que "hablen" del punto D. Ellas dicen: |
|
|
|
| Estas son las ecuaciones que describen TODO el movimiento delineado en el enunciado. |
| |
 |
1800 m = ½ a (30 s) ² |
|
| vD = a . (30 s) |
|
|
|
|
| Estas dos, en cambio, hablan exclusivamente del punto D. |
| |
Fantástico, quedó un sistema de dos ecuaciones con dos incógnitas. Acá terminó la física del problema. El resto es álgebra y no es tan peliagudo. Igual te ayudo: de la primera ecuación despejo a. Obtengo
a = 4 m/s²
este valor lo meto en la segunda ecuación y calculo la velocidad en el despegue. |
|
|
|
|
|
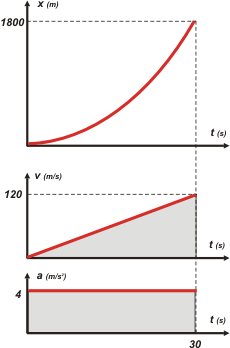
| Vamos a hacer los gráficos. |
|
|
|
|
|
|
Fijate: siempre los hago encolumnados, con la misma escala de tiempo y en el mismo orden: posición, velocidad, aceleración.
Prestale atención a la parábola: arranca sin inclinación (eso representa que la velocidad inicial es nula).
Sin hacer ningún tipo de cálculos, decir (sin repetir y sin soplar) cuánto valen las áreas sombreadas. (Si no se te ocurre, entonces, bueno, calculalas... ¡y avivate!). |
DESAFIO: Tomar como constantes "iniciales" las del punto de despegue D. (Resultados: los mismos). |
|
 |
| Algunos derechos reservados (en criollo: no podés publicarlo a tu nombre, ¿entendiste?).
Se permite su reproducción citando la fuente. Última actualización ago-06. Buenos Aires, Argentina. |
|
|
| |
|

