 |
NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Movimiento uniformemente variado)

|
|

|
NMS c3.31* - Desde el borde de un acantilado de 50 m de altura se lanza un cuerpo verticalmente hacia arriba con 10 m/s y simultáneamente se arroja otro hacia abajo desde la misma posición con 10 m/s, entonces cuando el primero llega a su altura máxima, la distancia entre ambos es:
a) 5 m b) 15 m c) 20 m d) 30 m e) 25 m f) 0 m |
|
| *Este ejercicio formó parte del examen libre tomado en dic/13. Para ver el tema de examen entero hacer click acá. |
|
|
|
De todas las herramientas cinemáticas, el esquema es la más idónea para organizar la información, para dar la idea general del movimiento con un solo golpe de vista. Aquí va. (No olvides la estadística: con un esquema completo y bien hecho tenés un 97,4 % de probabilidades de resolver bien el problema; y con un esquema ausente, o incompleto, o con errores, o demasiado desprolijo... tenés un 97,4 % de fracasar en la resolución del problema). |
|
|
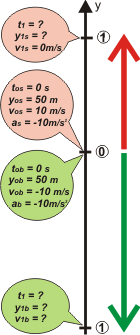 |
Mirá este esquema. Está completo, prolijo y tiene todos los chiches. Le puse subíndice s al cuerpo que inicalmente sube y b al que baja.
Look at the signo que le puse a las velocidades iniciales, y súper ojímetro al signo de las aceleraciones de cada cuerpo... ¡los dos tienen el mismo signo!
Bien, como siempre, escribiremos las ecuaciones horarias para cada cuerpo. ¿Tenés las ecuaciones generales a mano?
y = yo + vo ( t – to ) + ½ g ( t – to )²
v = vo + g ( t – to )
Reemplacemos en ellas las constantes iniciales (to , yo , vo y a) por las constantes iniciales de cada piedrita. Las ecuaciones quedan así: |
|
|
Cualquier otro sistema de referencia hubiera sido igualmente válido |
| cuerpo que sube |
ys = 50 m + 10 m/s . t – 5 m/s² . t² |
| vs = 10 m/s – 10 m/s² . t |
| cuerpo que baja |
yb = 50 m – 10 m/s . t – 5 m/s² . t² |
| vb = – 10 m/s – 10 m/s² . t |
|
|
Estas son las ecuaciones que describen TODO el fenómeno del movimiento contado en el enunciado. |
| Ahora usémoslas. Pidámosles que "hablen" del instante que nos interesa, el 1, cuando el cuerpo que sube alcanza su altura máxima. Ellas dicen... |
|
|
 |
ys1 = 50 m + 10 m/s . t1 – 5 m/s² . t1² |
[1] |
| 0 m/s = 10 m/s – 10 m/s² . t1 |
[2] |
| yb1 = 50 m – 10 m/s . t1 – 5 m/s² . t1² |
[3] |
| vb1 = – 10 m/s – 10 m/s² . t1 |
[4] |
|
|
Estas, en cambio, son las ecuaciones especializadas para los instantes que a vos te interesan. |
La ecuación [4] (velocidad del cuerpo que baja, cuando la que sube alcanzó su altura máxima) no nos interesa. Ahora... fijate que las otras 3 arman un sistema de tantas ecuaciones como incógnitas (3x3)... por eso le dibujé una llave y descorché una sidra porque la distancia entre cuerpos (ys1 – yb1) ya lo podemos calcular... ¡sólo es álgebra! No llores, yo te lo hago.
De la [2] despejamos t1 y lo calculamos.
t1 = 10 m/s / 10 m/s²
t1 = 1 s
Con ese valor vamos a la [1] y a la [3] y calculamos las posiciones (hacelo vos).
ys1 = 55 m
yb1 = 35 m
Salió con fritas:
ys1 – yb1 = 55 m – 35 m
|
|
|
| |
ys1 – yb1 = 20 m |
opción c) |
|
|
|
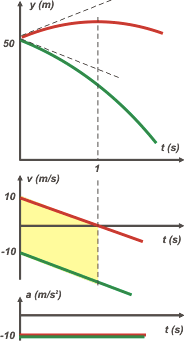 |
Los hice con mucho esmero para que los observes con detenimiento. El cuerpo que inicialmente sube, con curvas rojas; el cuerpo que baja, curvas verdes. Mirá cuántos detalles a los que tenés que prestar atención:
¿Qué característica importante tiene la curva de posición roja en el instante 1?
¿Qué te querrán mostrar esas dos rectas punteadas oblicuas que puse en el gráfico de posiciones?
¿Por qué las gráficas de velocidad de ambas piedras las hice paralelas?
¿Cuánto podrá valer el área que coloreé de amarillo? |
|
|
|
| Eso era todo lo que se me ocurre. Debe haber más. |
|
|
| DESAFIO: Para responder mentalmente y en menos de 1 segundo... ¿cuánto vale la velocidad del cuerpo que baja cuando el que inicialmente sube llegó a la altura máxima? |
|
|
| Prohibida la reproducción total o parcial de este material didáctico extraordinario por cualquier medio visual, gráfico, sonoro u holográfico. Las transgresiones a esta disposición serán penalizadas con 32 clases de "El ello y el superyó en la formación de la personalidad neurótica" de Psicología Medieval.
Sólo se permite su reproducción citando la fuente. Algunos otros derechos reservados. Última actualización ene-14. Buenos Aires, Argentina. |
|
|
|

