home  | más de cinemática | otros temas de Física | lecciones del maestro Ciruela | tonterías |  @ 
NO ME SALEN
EJERCICIOS RESUELTOS DE FÍSICA
(Movimiento rectilíneo uniformemente variado)

 

manolito
NMS c3.18 - Una joven de singular belleza va en bicicleta por una calle, con una marcha regular qule permite recorrer una cuadra (100 m) en la tercera parte de un minuto. Al pasar por una esquina, un motociclista que se encontraba allí queda deslumbrado durante 10 segundos y luego incia su persecusión con aceleración constante a través de 2 cuadras empleando para ello 20 segundos, y luego se detiene allí bruscamente. a) ¿cuál es la velocidad de la ciclista?; b) ¿cuál es la aceleración del motociclista durante su carrera?; c) ¿adónde se detiene el motociclista?; d) realice una representación gráfica de la velocidad en función del tiempo para ambos vehículos; e) realice una representación gráfica para la posición en función del tiempo de ambos vehículos; f) ¿cuántas veces se encuentran ambos en los recorridos descriptos?; g) obtenga los tiempos y posiciones donde ocurren los encuentros. *

¡Puaj! ¡Qué cantidad de preguntas infernal! Pero tienen su lógica. Si tenés un minuto te la cuento. Se trata de una técnica viejísima que se llama "ejercicio guiado" y consiste en que la serie de preguntas formuladas constituye una guía de resolución del ejercicio. En mi opinión, un ejercicio presentado de esa manera pierde valor, porque en este caso no es más que un reemplacismo oficializado. No me salen va a resolver este ejercicio con su método habitual, robusto, masivo, poderoso y vas a ver cómo todas las incógnitas se resuelven de una y la guía para tontos era innecesaria.

El ejercicio es tan simple que te voy a ahorrar el esquema. De todos modos hay que fijar el SR y darle nombre a las variables. Acá va:

SR: Voy a tomar como cero de los tiempos el instante en que la ciclista pasa por la esquina donde está parado el motociclista. El cero de las posiciones, también ahí. Sentido creciente el mismo que los movimientos.

Si te queda alguna duda podés ir a los gráficos que están más abajo y te las sacás.

En base a esta elección, las 3 ecuaciones que describen todo el ejercicio serán éstas:

    
ciclista x = vc . t  
moto

x = ½ a (t — 10s)²

  
moto vm = a (t — 10s) pero no la voy a usar
  PASO DOS
ARMAR
LAS ECUACIONES
La tercera ecuación, que describe las velocidades de la moto en todo instante de tiempo, no voy a usarla... aunque si lo hiciese no perderíamos nada. Las otras dos sí: a la de la ciclista le vamos a pedir que hable de los dos puntos interesantes (y mencionados en el enunciado): el pasaje por la esquina siguiente (100 m) y el encuentro (e). Y a la del baboso motociclista le pido que hable también de los dos eventos mencionados, la llegada a la segunda esquina (200 m) y el encuentro (e).    
ciclista en 100 m 100 m = vc . 20 s [1]
ciclista en e xe = vc . te [2]
moto en 200 m

200 m = ½ a (30s — 10s)²

 [3]
moto en e xe = ½ a (te — 10s)² [4]
  PASO TRES
USAR
LAS ECUACIONES

Y como siempre... desembocamos en un sistema de ecuaciones con tantas ecuaciones como incógnitas... ¡aleluya, hermano!, ¡aleluya!... hemos resuelto el ejercicio... por lo menos la física del ejercicio que era lo que me interesaba. El resto es álgebra, y bastante sencillita por cierto. Rsolvamos por este camino (que no es el único). De la ecuación [1] despejamos y calculamos la velocidad de la piba.

vc = 100 m / 20 s

    
 

           vc = 5 m/s

  
   

De la ecuación [3] despejamos y calculamos la aceleración del repartidor de pizza (que se piensa que ese bomboncito le va a dar bola...).

a = 2 . 200 m / (20s)²

a = 400 m / 400s²

    
 

           a = 1 m/s²

  
   

Las otras dos ecuaciones, la [2] y la [4], las igualo para que desaparezca una incógnita (xe) y poder encontrar la otra ( te).

vc . te = ½ a (te — 10s)²

Para hallar el valor de la incógnita hay que operar un poco. Acordate ese asunto del cuadrado de un binomio...

vc . te = ½ a (te² — 20s te + 100s²)

Ahora paso el término del primer miembro al segundo, y agrupo.

0 = ½ a te² — ½ a . 20s te + ½ a . 100s² — vc te

0 = ½ a te² — (½ a . 20s + vc ) te + ½ a . 100s²

Reemplazo a y vc por los valores hallados antes y lo que nos queda es ésta ecuación cuadrática:

0 = 0,5 m/s² te² — 15 m/s te + 50 m

Que se resuelve aplicando la formulita de los griegos... y que arroja dos soluciones para la incógnita, que llamaré te1 y te1'. Los valores numéricos dan:

te1 = 26,18 s        y        te1' = 3,82 s

No cabe duda de que el resultado que tiene sentido es te1 y el otro debemos descartarlo. Con ese valor volvemos a las ecuaciones horarias de los chicos y nos fijamos en qué posicion se encuentran:

    
 

           te1 = 26,18 s        xe1 = 130,9 m

  
   

Hay un segundo encuentro, siempre y cuando el chico no haya dicho ninguna grosería y la piba siga pedaleando. Si leés bien el enunciado, la pregunta es trivial:

    
 

           te2 = 40 s        xe2 = 200 m

  
   
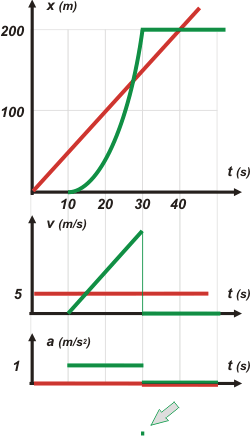
Ahora vamos (como siempre) a los gráficos. Yo lo hubiera hecho de entrada en forma cualitativa al menos; pero ya que lo hacemos al final ponemos datos numéricos:    

La piba en rojo y el tonto en verde. Acá se ven perfectamente los dos encuentros. Fijate la correspondencia que hay entre los tres gráficos que, como siempre, confeccioné en tándem.

Algunos detalles interesantes: en el gráfico de velocidad del motociclista, en el instante 30 segundos que es cuando llega a la segunda esquina y se prepara para el segundo encuentro, el enunciado decía: se detiene allí bruscamente. Bien, resulta que nuestro universo no permite saltos de velocidad, o sea, que si bruscamente paso de una velocidad a otra, el universo me obliga a pasar por las infinitas velocidades intermedias, de corrido, de continuo. Por eso le hice una rayita vertical (casi vertical) verde más finita.

El universo en cambio, sí permite saltos de aceleración, por eso dibujé un punto verde (flecha) a los 30 segundos que representa la aceleración (negativa en este caso) que debe haber tenido la moto para poder frenar. Seguramente el módulo de esa aceleración es mucho más grande del que representé en el gráfico... pero al menos aparece.
   
(*) Este ejercicio perteneció al primer examen parcial de Física del CBC de 1991.
   

DESAFIO: Ya habíamos discutido que el segundo valor para instante de encuentro que nos había tirado la resolución de la cuadrática, te2 = 3,82 s, no tenía sentido, pero... qué explicación puede tener, ¿cómo las matemáticas pueden respondernos un sinsentido y nosotros tan panchos?

  Ricardo Cabrera
Algunos derechos reservados. El uso de ste material didáctico está mal visto por la Asociación Internacional de Pedagogos de todo el universo. Se permite su reproducción citando la fuente. Última actualización abr-10. Buenos Aires, Argentina.