home  | más de cinemática | otros temas de Física | lecciones del maestro Ciruela | tonterías |  @ 
NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC


  

manolito

NMS c3.09* - Un cuerpo que desciende en caída libre pasa por los puntos A y B de su trayectoria con velocidades vA = 20 m/s y vB = 50 m/s. Hallar la distancia AB.

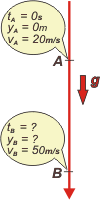
Esta vez dejame que yo elija el SR. Te lo muestro en un esquema, por supu. Mirá cómo todas las cosas que intervienen en el problema ya tienen nombre a partir del esquema. Si, por algún motivo, durante el desarrollo, me pierdo o me olvido de algo... al esquema me remito: ahí está todo.

Buscá los modelos de ecuaciones horarias que se usan en estos casos, en los que se trata de un movimiento variado con aceleración g = 10 m/s² (¡POSITIVO!, ya que elegí un SR con sentido positivo hacia abajo).

Si tomamos el punto A como "inicial" en este movimiento, las constantes para la ecuación horaria (to, yo, vo y a) están todas agrupaditas y ordenaditas junto al punto A. Las reemplazamos, y nuestras ecuaciones quedan listas para ser usadas.

Son muchos los que cuando quieren hacer este problema no resisten la tentación de poner el punto inicial en algún supuesto punto desde el cual supuestamente el objeto supuesto se supone que se suelta desde el reposo, es decir, con velocidad inicial cero, y no se dan cuenta de que tantas suposiciones son al reverendo supuesto. De todas formas, después te desafío para que lo rehagas de ese modo.
 


y = 20 m/s . t + 5 m/s² . t²

v = 20 m/s + 10 m/s² . t
Estas son las ecuaciones que describen TODO el movimiento
Como siempre, las ecuaciones horarias las escribo como tales, es decir, no reemplazo las variables (y y t, v y t, en este caso); sí las voy a reemplazar cuando las "use", especializándolas para que "hablen" de algún punto en particular. Ahora mismo, por ejemplo, les pido que hablen del punto B. Miremos lo que dicen:  
yB = 20 m/s . tB + 5 m/s² . tB² [1]
50 m/s = 20 m/s + 10 m/s² . tB [2]
 

¡Aleluya! Apareció un sistema de tantas ecuaciones como incógnitas (esto me parece una historia repetida). Su solución es muy sencilla y estoy seguro de que no es necesario que te la muestre... pero es mi oficio. De [2]

tB = ( 50 m/s – 20 m/s ) / 10 m/s² = 3 s

Ahora con eso voy a [1]

yB = 20 m/s . 3 s + 5 m/s² . 9 s2

yB = 105 m

  
 

        AB = yB – yA = 105 m

        (Qué lo parió)

 
DESAFIO: Rehacer el problema pero con otros dos SR: uno que apunte hacia abajo y tenga el cero de los tiempos y de las posiciones en el instante en que la velocidad era nula; y el otro que apunte hacia arriba y tenga el cero de posición en el piso (no importa cuánto más abajo de B).  
  Ricardo Cabrera
* Este problema pertenecía a la guía de problemas de la materia Fisica, que se usó hasta el año 2003. Se trataba del ejercicio 3.22.
 
Prohibida la reproducción total o parcial de este material didáctico extraordinario por cualquier medio visual, gráfico, sonoro u holográfico con fines comerciales. Las transgresiones a esta disposición serán penalizadas con 18 clases iguales de "ecuación de los gases ideales" de Química del CBC. Sólo se permite su reproducción citando la fuente. Última actualización ago-06. Buenos Aires, Argentina.