 |
NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Movimiento uniforme)
|
|

|
 |
NMS c2.03 - Dos participantes de una carrera de regularidad trazaron cada uno el gráfico de posición en función del tiempo de su vehículo, desde sus propios sistemas de referencia (gráficos A y B) para un tramo recto de su recorrido. |
| |
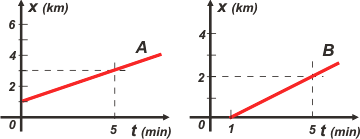 |
a - Escribir las ecuaciones horarias de cada vehículo, desde el sistema elegido por cada participante.
b - ¿Se puede decir cuál de ellos se movió a mayor velocidad?
c - Hallar la posición de cada vehículo en tA= tB= 15 minutos. ¿Se puede afirmar que están juntos en ese instante? ¿Por qué? |
|
| |
|
|
Vamos con la A. La consigna es armar la ecuación horaria. Busquemos el modelo de ecuación que tenemos que armar... Se trata de un MRU, no cabe duda... Acá está:
x = xo + v ( t – to )
Para armarla tenemos que buscar las tres constantes: to, xo y v. ¿Nos da el gráfico esa información? A ver si nos ponemos de acuerdo en qué información nos da el gráfico exactamente. Volquémosla a una tabla de valores. |
|
|
|
Para hallar v usaremos el concepto de velocidad media, ya que para el MRU velocidad y velocidad media coinciden perfectamente: v = vm = ΔX / Δt. Esto implica que tenemos que tener un desplazamiento y el intervalo de tiempo correspondiente. Justo lo que tenemos. |
|
|
|
ΔX = 3 km – 1 km = 2 km
Δt = 5 min – 0 min = 5 min
|
|
|
| vA = |
|
Δx |
= |
2 km |
= 0,4 km/min |
|
|
| Δt |
5 min |
|
|
|
¿Quiénes serán to y xo?, parecen ser 1 km y 0 min. Pero también podrían ser 5 km y 5 min. Qué dilema... cualquiera de los dos sirve. Elijamos el primer par. |
|
|
| |
x = 1 km + 0,4 km/min . t |
Móvil A |
|
|
|
Vamos con el móvil B. Operamos de manera idéntica.
|
|
|
|
ΔX = 2 km – 0 km = 2 km
Δt = 5 min – 1 min = 4 min
|
|
|
|
| vB = |
|
Δx |
= |
2 km |
= 0,5 km/min |
|
|
| Δt |
4 min |
|
|
|
| |
x = 0,5 km/min . ( t – 1 min ) |
Móvil B |
|
|
|
Aunque ambos observadores hayan elegido diferentes sistemas de referencia es fácil comparar las velocidades, ya que eligieron las mismas unidades. |
|
|
|
|
|
Ahora le pedimos a cada ecuación que nos diga dónde se hallaba el móvil en el instante minuto 15.
A → xA15min = 1 km + 0,4 km/min . 15 min
xA15min = 7 km
B → xB15min = 0,5 km/min . ( 15 min – 1 min )
xB15min = 7 km
|
|
|
|
|
|
| Pero no podemos afirmar que se hallen en la misma posición, porque no sabemos si ambos observadores tomaron el mismo instante como minuto cero de sus respectivos sistemas de referencia, ni tampoco qué posición tomaron como kilómetro cero. |
|
|
DESAFIO: ¿Qué gráfica debería tener mayor pendiente? ¿Qué gráfica debe estar más inclinada? |
|
 |
| |
|
| Algunos derechos reservados.
Se prohibe estrictamente leer este ejercicio resuelto por encima: hay que leerlo despacio y con atención. Las penalizaciones a esta infracción son severísimas. Se permite su reproducción citando la fuente. Última actualización abr-14. Buenos Aires, Argentina. |
|
|
| |
|

