NO ME SALEN
SOLVED PHYSICS EXCERCISES FROM THE CBC |
|

|
Aditional No me salen 1.9*. - An automovil heads North with a 20m/s speed; A minute after and 300 meters away from the first position, it started moving eastward, with a 20m/s speed. Then, the average acceleration modulus in that interval is:
a) 0 b) 0,33 m/s² c) 0,66 m/s²
d) 0,47 m/s² e) 0,08 m/s² f) 1 m/s²
This excercise is very simple, I chose it because it has some interesting points to analyze. Let´s see an schme where the mentioned speeds are shown. Here I added a reference system with two cartesian axes. |
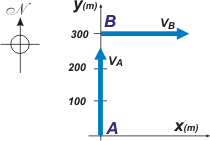 |
It´s first position is A. And it´s speed is vA
rA = 0 m î + 0 m ĵ
vA = 0 m/s î + 20 m/s ĵ
(see footnote). One minute after, you will find it at B, with a vB speed.
rB = 0 m î + 300 m ĵ
vB = 20 m/s î + 0 m/s ĵ |
|
|
|
Between A and B we have the timelapse...
ΔtAB = 1 min = 60 s
We have everything to solve this problem (and we even have data to spare)
amAB = ΔvAB / ΔtAB = vB — vA / ΔtAB
Let´s see what we are talking about when we mention ΔvAB. |
|
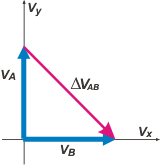 |
There you have it: the pink vector, the one with ot´s origin in the end of the second one. It´s cartesian expression is:
ΔvAB = 20 m/s î — 20 m/s ĵ
To find the modulus is pretty easy now that you have the cartesian expression, you can use The Pitagoras Theorem.
|ΔvAB| = [ (20 m/s)² + (20 m/s)² ]½
|ΔvAB| = 28,28 m/s
|
|
|
| Then, the average acceleration modulus is: |amAB| = |ΔvAB| / ΔtAB |
|
| |
|amAB| = 0,47 m/s² |
Answer d)
|
|
|
There is another way to face this problem: obtain the cartesian expression of the average acceleration vector and then – the same way as before - calculate it´s modulus. Shall we do it?
amAB = ( 20 m/s /60 s) î — ( 20 m/s /60 s) ĵ
amAB = ( 0,33 m/s²) î — ( 0,33 m/s²) ĵ
Check this, we reached the same conclusion. That means I solved, I soo solved the excercise. But... now that you have reached this far, keep reading a little bit that the best part is coming: I´m going to talk to you about the spooky and malicious trap us teachers set.. guaaagh!!!
To begin, read again the statement and agree with me: the position B is not necessarily de one I portrayed in the first scheme. The statement says ``300 meters away from the first position´´... This can be 300m to the North or any other direction. The movil´s trajectory - even though the statement alludes to a straight line trajectory - It can be any, while it fulfills that the speeds are tangent to them. Here are a couple of possibilities. |
|
|
|
I´ve drawn two trajectories in red, two of the infinite amount of possibilities there are. I´m going to work a little with the one at the right, since it is more usefull now that I can show you clearly the displacement vector, ΔrAB. There you have it, in green. It doesn´t matter where I point to, the displacement modulus is 300 m (the statement agrees)... but here you can crystañ-clear see that non nummerically, non vectorially, non nothing has anything to do with the speed variation, ΔvAB. The 300 m things is Olympian-out of place.
But it wouldn´t have been out of place to use it. I would, too. To know physics implicates to know which elements of the universe to use, and wich not. If the cutout was made by the teacher, and not you, the question would be a silly one, like asking wich color was San Martin´s white horse (well, not sooo silly) (btw, this is considered a really stupid question, the answer is supposed to be ``dark brown´´ but there are no solid sources about this, the paintings in this white horse are misinterpreted sometimes and some people claim there was not even a horse to begin with, so, please imagine a silly question). For the ``realistic´´ effect having some sense, between the options, here should be those that poorly choose the incorrect elements.. |
|
| * This excercise was part of the first midterm exam taken at University ciry, at the noon time band, tuesdays and fridays. |
|
 |
| |
Note: î and ĵ are vectors of modulus 1, also called "Versors" , their objetive is to join the vectorial characteristics of a number and tell where it is pointing to. Usually it is portrayed with a little hat or a little comma above (replacing the typical i and j ) . Versor î has the same direcction and sense in the x axis, as the ĵ versor in the y axis.
CHALLENGE: why does the average acceleration can never be 0? |
|
| |
| Some Rights Reserved. Not allowed to be copied without naming either the author or this source material. Those ones not obeying these rules will be sentenced to hard labor in the Antarctica. Translated by Santi Pisci. Last updated ago-15. Buenos Aires, Argentina. |
|
|
|

