NO ME SALEN
THEORETICAL NOTES AND EXCERCISES OF PHYSICS AND BIOPHYSICS
(vectorial kinematics) |
|

|
 |
NMS 1.6- A saloon with rectangular faces has the next dimensions: 12m x 4m x 3m. A fly takes off from a corner and reaches de diametrically opposed corner in 6.5 seconds. Determine the fly´s average speed, and it´s modulus. Challenge: if the fly moves by walking on the walls at a rate of 1cm/s, how much time it would take as minimum to walk from one corner to the diametrically opposite corner? |
|
This excercise is so dumb that we never solve it in class, and the students usually read the statement and skip to the next excercise. Let´s do this: we will try and squeeze it as much as we can.
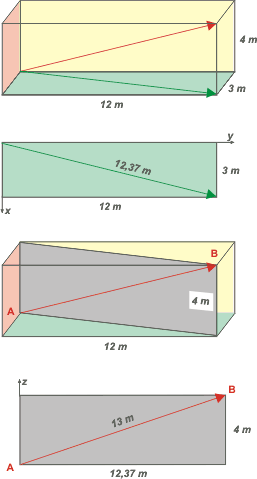
Let´s begin with a position scheme, this will allow us to define some things. Here you have: |
|
|
 |
This representatios of the saloon is not the only possible one, but the results should be the same regardless of the case we choose. I colored the internal walls and the floor; and the external walls and the roof are transparent. |
|
|
|
Also, i put a tridimensional reference system (x, y, z) so you see one for the first time in your life. With this, we can define the final and the initial positions of the fly and it´s displacement. A possible notation would be: coordinates of point A: (0; 0; 0),and the ones from point B: (3; 12; 4). This way we can portray de position vectors:
rA = 0 m î + 0 m ĵ + 0 m k'
rB = 3 m î + 12 m ĵ + 4 m k'
î, ĵ and k' are vectors mof modulus 1, also called "Versors", their objetive is to join the vectorial characteristics of a number and tell where it is pointing to. Usually it is portrayed with a little hat or a little comma above. Versor î has the same direcction and sense in the x axis, as the ĵ versor in the y axis, and the k' in the z axis. (I don´t have the hatted k, wich would be the correct one).
The ΔrAB displacement is found by subtracting the position vectors.
ΔrAB = rB — rA = 3 m î + 12 m ĵ + 4 m k'
The avergage speed, vm = Δr / Δt,is found by dividing each component (each term) by the corresponding time interval, in this case 6.5 s.
vm = 0.46 m/s î + 1.85 m/s ĵ + 0.62 m/s k'
However, in this excercise, the authors want us to obtain the average speed and that is a thing we can accomplish using lots of different methods; One is the pithagorical:
|vm| = [ (0.46 m/s)² + ( 1.85 m/s)² + ( 0.62 m/s)² ]½
Other way is obtaining the displacement modulus and then divide it by the time interval: That is: |vm| = |ΔrAB| / Δt. I´m interested in expanding this idea, because I want to show you how to find the value of the saloon´s principal diagonal |
|
exponente ½ es lo mismo que
raíz cuadrada |
|
 |
Again, there is not only a single way, but I will walk through a very common path that will lead us to a very important lesson.
Look at the diagonal in the floor (of, if you want, the shadow of the displacement vector in the ground): we can obtain it´s value using Pitagoras, since that diagonal divides de floor in two rectangle triangles, where the diagonal is the hypotenuse and the hicks are 12 and 3 meters respectively. Knowing this, the hypotenuse is:
dxy = (12² + 3²)½ = 12.37
Now look at the light blue rectangle, it is vertical according to the diagonal in the floor. If we follow this the same way as we did before, with Pitagoras... we have:
|Δr| = (12,37² + 4²)½ = 13
If tou look, this is tha same that
|Δr| = (3² + 12² + 4²)½ = 13
That is, a tridimensional Pitagoras. |
|
|
If we go back to the definition of average speed:
|vm| = |Δr| / Δt =
|vm| = 13 m / 6.5 s
|
|
|
|
| CHALLENGE: this time the challenge is promoted by the book, so we can´t turn it down. Besides I think can win against the book, because No me salen has a shorter path for the walking fly. How have I found it? Easy: the shortest way between two points is a straight line, I know, the walls and the floor are folded, I can´t travel through a straight line... What i´d done was to unfold the saloon, like cardboard. |
|
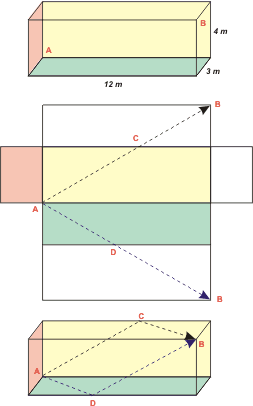 |
Moreover, i´ve found to different paths, with equal lenghts and the two shorter than the one in the book.
Look at how I unfolded the saloon. Point B is distributed in two places, both at the same distance from A.
How much is that distance? By a simple Pitagoras, I don´t know you, but I see two rectangle trangles. Both have a 12 meter base and a height of (4+3) 7 meters,thus, the hypotenuse, that is no other than the path our desalinated fly has to walk by, is
dmín = (12² + 7²)½ = 13,89
all in meters, of course.
Δt = dxyz / 1 cm/s
Δt = 1.389 cm / 1 cm/s |
|
|
| This means, the fly can walk through the floor until point D and then climb until it reaches point B. Or climb the internal wall until it reached point C and then walk through the ceiling until it reaches B. |
|
|
|
|
|
|
|
| |
| SECOND CHALLENGE: even if this excercise has a huge component of geometry and the other little component is kinematics, strenghtening some knowledge won´t hurt. Geometry is essential for all the physics course. I challenge you - if you dare- yo locate de position of points C and D, determine the angle our fly must displace in both walking and flying sections. |
|
 |
| |
| Some rights reserved. Reproduction allowe by quoting the source. Translated by Santi Pisci. Last Updated jul-15. Buenos Aires, Argentina. |
|
|
|

