 |
NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Vectorial kinematics) |
|

|
 |
NMS 1.5- A running track consists in two straight stretches, each one with a lenght of 80m, and two stretches, giving form to a semi-circumference. The straight stretches are separated one another by a distance of 40m, this way, the semi-circumferences at it´s ends has a 20m radius. A runner runs it with constant speed modulus 18km/h. |
a- Draw the track; portray the instant speed vectors: - in the straight stretched midpoints (A and C - in the curved stretches midpoints (B and D).
b- Find the time it took the runner to complete one lap, and how much it took to reach B from A and C from A.
c- Determine the average acceleration vector of the runner between A and C, and between C and D.
d- Indicate both direction and sense of the instant acceleration vector in every single remarkable point (A, B, C and D).
e- Find the average speed vector in an entire lap between A and A, and the scalar average speed between those points. |
|
This excercise has it´s questions in the right order. |
|
|
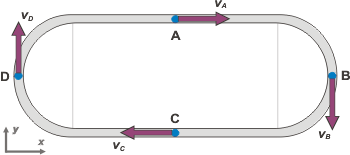 |
Some security measures I took to portray the speeds are: the lenght of the arrows for the speed must be the same (because speed in this case is constant), |
|
|
|
second, the direction of the vectors is always (not just in this excercise) tangent to the trajectory.
I´m going to express the speed in meters over second, since I will need it for future calculations. If you do not remember how to do convertions, you might as well like to check this first. Then, 18 km/h = 5 m/s , so:
vA = 5 m/s î
vB = — 5 m/s ĵ
vC = — 5 m/s î
vD = 5 m/s ĵ
î y ĵ son vectores de módulo 1, se llaman versores y tienen por objeto contagiar el carácter vectorial a un valor numérico y decir para dónde apunta. Suelen representarse con un sombrerito o una comita arriba (en lugar del punto típico de la i y la j). El versor î tiene la misma dirección y sentido que el eje x, y el versor ĵ que los del eje y.
To answer the second item, we must "right", the track... or what is the same, imagine the track as the sum of the two straight stretches and the two curved ones, that eqials to Δx = 286 m. (Remember: the lenght of the curved stretch is equal to more or less, 3,14 times the diameter). Then:
Δt = Δs / v
Δt = 286 m / 5 m/s
|
|
|
|
|
The average acceleration vector in each segment is obtainable by operating with the speed vectors above, see for yourself:
amAC = ΔvAC / ΔtAC =
amAC = (vC — vA) / ΔtAC =
amAC = (— 5 m/s î — 5 m/s î) / 28s =
amAC = — 0,35 m/s² î
This way you also obtaing
amBD = 0,35 m/s² ĵ
Now that we are here, we could also obtain some extra average accelerations... for example:
amAA' = 0
Or this one, a more intriguing one
amAB = (— 5 m/s î — 5 m/s ĵ) / 14s =
amAB = — 0,35 m/s² î — 0,35 m/s² ĵ
Wich modulus is
|amAB| = 0,50 m/s²
I´ll just square up the ones they asked for: |
|
| |
amAC = — 0,35 m/s² î
amCD = 0,35 m/s² î + 0,35 m/s² ĵ |
c) |
|
|
| I re do the scheme to portray the instant acceleration vectors mentioned in d- |
|
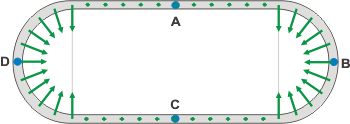 |
Some security measures I took to portray the instant accelerations are: if the speed is constant (in modulus and direction) then the acceleration is null (green dots mean that the acceleration is null). |
|
|
Then, in the segments where the speed changes it´s direction, the acceleration always (not just in this excercise) point towards the concavity of the trajectory, towards "inside", and for the end - even though you must not know about this, yet- if the speed´s modulus is constant but it´s direction changes, then the acceleration vector is perpendicular to the trajectory.
And now, it comes the item e-. To find the average speed vectors, we do the following:
vmAA' = ΔrAA' / ΔtAA'
vmAA' = 0 m / 57s
|
|
|
|
As you can see, the average speed vector is not very representative of what our fellow runners are doing on the track... It´s a lot more practical to calculate the scalar average speed:
vmAA' = ΔsAA' / ΔtAA'
vmAA' = 286 mm / 57s
|
|
|
|
| (Thing we alreadky knew). The vectorial speed and the scalar speed differ from each other with a little arrow (a hat-ish arrow-like ) on the vectorial one... but that in HTML language, for INTERNET, is not very practical. I owe you. |
|
| |
|
|
|
|
|
| |
| CHALLENGE: Portray in a graph, the average acceleration vectors in item c- . If you know how to do it, draw them in a proportional scale to the acceleration vectors of the second scheme. If you do not know how to do it, it does not matter, the point is that you see them pointing in the right direction. |
|
 |
| |
| Some rights reserved. Reproduction allowe by quoting the source. Translated by Santi Pisci. Last Updated jul-15. Buenos Aires, Argentina. |
|
|
|

