CINEMATICA, Guia 1 Ej 05, practica online de fisica

home

más de cinemática

otros temas de Física

lecciones del maestro Ciruela

tonterías

NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Cinemática vectorial)

NMS 1.5- Una pista de atletismo consiste en dos tramos rectos paralelos, de 80 m de longitud cada uno, y dos tramos en forma de semicircunferencia, que los conectan por sus extremos para cerrar el circuito. Los tramos rectos están distanciados entre sí 40 m, de modo que los tramos curvos tienen 20 m de radio. Un corredor la recorre con una velocidad de módulo constante e igual a 18 km/h.

        a - Hacer un esquema de la pista; representar los vectores velocidad instantánea del corredor: - en los puntos medios de los tramos rectos (Puntos A y C) - en los puntos medios de los tramos curvos (Puntos B y D).
        b - Hallar cuánto tiempo tardará en recorrer el circuito completo, y cuánto para ir de A hasta B, y de A hasta C.
        c - Determinar el vector aceleración media del corredor entre los puntos A y C, y entre C y D.
        d - Indicar la dirección y el sentido del vector aceleración instantánea en cada uno de los puntos indicados.
        e - Hallar el vector velocidad media en un recorrido completo entre A y A, y la velocidad escalar media entre esos puntos.

Este ejercicio tiene sus preguntas en el orden indicado.

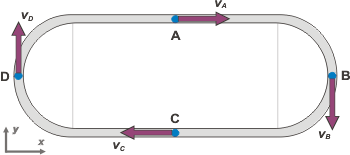Los principales recaudos que tomé para representar las velocidades fueron: primero, que el largo de las flechitas fuera igual en todas, ya que el módulo de la velocidad (la rapidez) es constante.

Segundo, que la dirección de los vectores fuera siempre (no sólo en este ejercicio) tangente a la trayectoria.

Con esto liquidamos el ítem a), pero podemos hacer algo más, todavía. Podemos hacer una representación analítica de las velocidades en esas cuatro posiciones. Para eso incluí en el esquema un par de ejes que servirán de sistema de referencia.

Voy a expresar la velocidad en metros sobre segundo ya que más adelante lo voy a necesitar para otras operaciones. Si no te acordás cómo se hacen los pasajes, podés consultarlo acá. Como 18 km/h = 5 m/s, tenemos:

v_A = 5 m/s î

v_B = — 5 m/s ĵ

v_C = — 5 m/s î

v_D = 5 m/s ĵ

Donde î y ĵ son vectores de módulo 1; se llaman versores y tienen por objeto contagiarle el carácter vectorial a un valor, y decir para dónde apunta. Suelen representarse con un sombrerito o una comita arriba de la letra original . El versor îtiene la misma dirección y sentido que el eje x, y el versor ĵ los mismos que el eje y.

Para responder el segundo ítem tenemos que "rectificar" la pista o -lo que es lo mismo- pensar el recorrido escalarmente. La longitud del recorrido es la suma de los dos trayectos rectos más los dos curvos. Eso me da tanto como Δx = 286 m. (Recordá que la longitud de una circunferencia es más o menos igual a 3,14 veces el diámetro). Entonces

Δt = Δs / v

Δt = 286 m / 5 m/s

Δt = 57s

El vector aceleración media en cada tramo resulta de operar con los vectores velocidad que expresé más arriba, de la siguiente manera:

a_mAC= Δv_AC / Δt_AC =

a_mAC= (v_C — v_A) / Δt_AC =

a_mAC= (— 5 m/s î — 5 m/s î) / 28s =

a_mAC= — 0,35 m/s² î

y de la misma manera obtenés

a_mBD= 0,35 m/s² ĵ

Pero ya que estamos podemos calcular algunas aceleraciones medias más... por ejemplo:

a_mAA'= 0

O esta otra que es más interesante:

a_mAB= (— 5 m/s î — 5 m/s ĵ) / 14s =

a_mAB= — 0,35 m/s² î — 0,35 m/s² ĵ

cuyo módulo vale

|a_mAB| = 0,50 m/s²

Esperá, que recuadro los solicitados:

a_mAC= — 0,35 m/s² î

a_mCD= 0,35 m/s² î + 0,35 m/s² ĵ

Repito el esquema para representar los vectores aceleración instantánea que nos solicita el ítem d):

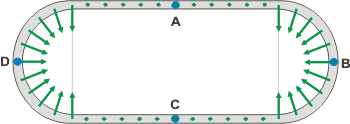Los principales recaudos que tomé para representar las aceleraciones instantáneas fueron: si la velocidad es constante (en módulo y dirección) entonces la aceleración es nula (hice puntitos verdes en varias posiciones para indicarte eso).

Luego, en las partes donde la velocidad cambia de dirección, la aceleración siempre (no sólo en este ejercicio) apunta hacia la concavidad de la trayectoria, hacia "adentro". Y por último -aunque esto no tenés por qué saberlo, todavía- si el módulo de la velocidad es constante pero cambia la dirección, entonces el vector aceleración es perpendicular a la trayectoria.

Y ahora viene el ítem e). Para hallar los vectores velocidad media, operamos de la siguiente manera:

v_m_AA' = Δr_AA' / Δt_AA'

v_m_AA' = 0 m / 57s

v_m_AA' = 0 m/s

Como ves, el vector velocidad media no es muy representativo de lo que hacen nuestros corredores sobre la pista... Es mucho más práctico calcular la velocidad escalar media:

v_m_AA' = Δs_AA' / Δt_AA'

v_m_AA' = 286 mm / 57s

v_m_AA' = 5 m/s

(Cosa que ya sabíamos). La velocidad vectorial y escalar se diferencian colocándole una flechita como sombrerito a la vectorial... pero hacer eso en el lenguaje HTML, para INTERNET, no es muy práctico. Te lo debo.

DESAFIO: Representar gráficamente los vectores aceleración media del ítem c). Si sabés cómo hacerlo, hacelos en una escala proporcional a los vectores aceleración que dibujé en el segundo esquema. Si no... no importa, basta con que los veas apuntando correctamente.