 |
NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Cinemática vectorial)
|
|
 |
 |
NMS 1.4- Un insecto pasa caminando por K
(rK = 2 cm î +
8 cm ĵ), con una velocidad
vK = — 8 cm/s î — 7 cm/s ĵ. Tres segundos más
tarde pasa por el punto L (rL= 11 cm î — 4 cm ĵ)
con velocidad vL= — 13 cm/s î + 5 cm/s ĵ.
a - En un esquema, trazar los vectores posición
y velocidad del insecto para ambos instantes.
b - Determinar los vectores desplazamiento,
velocidad media y aceleración media del insecto,
entre ambos instantes.
c - Dibujar una posible trayectoria. |
|
Mirá: no sé si lo hicieron a propósito o se les chispoteó, pero no es nada fácil representar todos esos vectores en un mismo gráfico porque se superponen unos a otros y si te tos dibuhjo todos de una, no vas a entender nada. De modo que lo voy a hacer en etapas y me parece, vas a entender un poco mejor. Acá va el primero. |
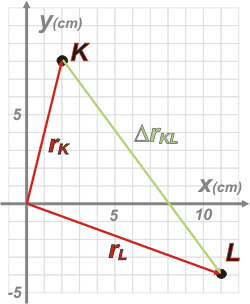 |
a - Te ubiqué los puntos K y L, y los vectores posición para ambos puntos:
rK = 2 cm î +
8 cm ĵ
rL = 11 cm î — 4 cm ĵ
Y el vector desplazamiento ΔrKL que se puede calcular fácilmente
ΔrKL = rL — rK
ΔrKL = 9 cm î — 12 cm ĵ
Habiendo transcurrido 3 segundos entre uno y otro, la velocidad media será:
vmKL = ΔrKL / Δt
vmKL = 3 cm/s î — 4 cm/s ĵ
|
|
|
|
î y ĵ son vectores de módulo 1, se llaman versores y tienen por objeto contagiar el carácter vectorial a un valor numérico y decir para dónde apunta. Suelen representarse con un sombrerito o una comita arriba (en lugar del punto típico de la i y la j). El versor î tiene la misma dirección y sentido que el eje x, y el versor ĵ que los del eje y.
Los vectores velocidad (tanto las velocidades reales en los puntos K y L -que son los que te da el enunciado del ejercicio- como el vector velocidad media que acabamos de averiguar) no pueden tener la misma escala que los vectores posición, que miden diferentes cosas, diferentes magnitudes, con diferentes unidades. Pero sí, en cambio, deben tener la misma dirección y sentido los representes el la escala que los representes. |
|
|
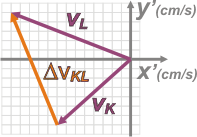 |
Una forma práctica de resolver el asunto es representar los vectores velocidad en un gráfico aparte y luego trasladarlos al gráfico de posición.
De paso, representé el vector cambio de velocidad, que me va a permitir calcular la aceleración media.
ΔvKL = vL — vK
ΔvKL = — 5 cm/s î + 12 cm/s ĵ
|
|
|
|
La aceleración media es el cociente entre el cambio de velocidad y el intervalo trancurrido durante ese cambio:
amKL = ΔvKL / Δt
amKL = ( — 5 cm/s î + 12 cm/s ĵ ) / 3 s
amKL = — 1,66 cm/s² î + 4 cm/s² ĵ
Que si tenés ganas de representarlo tendrías que hacerlo con otra escala arbitraria más, diferente a las anteriores... pero con las mismas dirección y sentido que ΔvKL. |
|
|
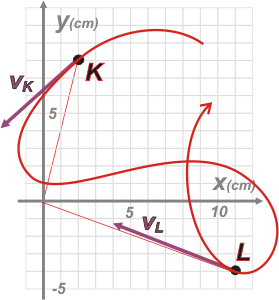 |
Bueno, acá aparece de nuevo el mismo gráfico del principio. Ves que en en punto K el vector posición y el vector velocidad (aún con escalas diferentes) se superponen casi perfectamente.
Los vectores posición los representé un poco más finitos para que no te molesten.
Dibujé una de las infinitas trayectorias posibles. Para dibujar una trayectoria tenés que tomar un único recaudo: la velocidad real siempre es tangente a la trayectoria. Y como ves: tanto en el punto K como en el L, me preocupé de que la velocidad y la trayectoria apunten para el mismo lado.
|
|
|
|
| Bueno, ya cumplí las consignas... un poco desordenado pero en aras de la claridad. |
|
|
DESAFIO: En base a la trayectoria que yo imaginé, trazá los vectores aceleración en K y en L (aceleración real, of course). |
|
 |
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Última actualización may-09. Buenos Aires, Argentina. |
|
|
|

