|
NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA
(Movimiento relativo)
|
|

|
| |
 |
FIS c7.04 - Two rams (a white and a black one) stand in front of each other, at a rest position, 24 m apart. In a given moment, both begin running towards each other. Considering constant accelerations of 1,6 m/s² y 1,4 m/s²respectively, and working from a reference system in which the white ram stands at a resting point, determine the kinematic equations for both rams with respect to that reference point and outline the corresponding graphs. |
|
Before tackling this exercise, I fervently recommend you to try and work out the solution to this same situation, but with a reference system set on the ground, and not on a moving body, here: c3.42
What is now proposed is to re-do that same exercise, but with a reference system that happens to be mounted on our white ram´s back and hanging on to his horns. This means that if he moves either here or there, his position will always be zero, always zero, is that clear enough? If our guy decides to take off at full speed and accelerate in order to crash against the black ram, he will always be fixed in the zero position of the reference system, with velocity=0 and acceleration=0… and the whole universe will be moving and accelerating, backwards… and don´t even get me started on what happens to the black ram!
Do not despair, there is always a way out. The mobile reference system that allows for movement within itself is the white ram´s imagination. It is the white ram. Therefore, we will work with: VBW, velocity of the black ram as seen by the white ram, VWG, velocity of the white ram, as seen from the ground, by a frightened observer. And at last, VBG, the velocity of our black ram, as seen by the same observer, on the ground. As always, it is true that
|
VBG = VBW + VWG
But… what about their accelerations? Same thing: if we divide this entire equation by the same time interval, we are left with:
aBG = aBW + aWG
|
 |
|
|
Carnero: Ovis aries. Macho de la oveja; rumiante ungulado que nunca hace paro; de la familia de los bovidae. |
As seen from the ground, the accelerations are the ones described in the exercise 3.12, which are aBG = – 1,4 m/s² and aWG = 1,6 m/s². Clearing this up, we get:
aBW = aBG – aWG
aBW = – 3 m/s²
This means that, as seen from the white ram´s position, who now feels like the center of the universe, the black ram is running backwards towards the center, towards him, with an acceleration of 3 m/s². It was only logical! I could´ve predicted this without knowing a thing about physics! |
|
|
Now, let´s build our black ram´s kinematic equations (since the white ram´s all equal zero, zero, zero).
x = 24 m – 1,5 m/s² . t2
v = – 3 m/s² . t
Asking these equations about the meeting point is the same as asking them to express the zero position, which is, of course, the white ram´s position, who is still insisting on being the center of the universe.
0 m = 24 m – 1,5 m/s² . te2
ve = – 3 m/s² . te
I knew it… two equations with two unknown variables. This setup is way easier than the original one! (The original exercise ended with a 4x4 equation system). From the first equation:
te² = 24 m / 1,5 m/s²
|
|
|
| |
te = 4 s |
The same result we got on the original problem! |
| |
|
Now, with this solution, we head to the second equation, and we are left with…
ve = – 3 m/s² . 4 s
|
|
|
| |
ve = – 12 m/s |
Same result as the original one? |
|
|
|
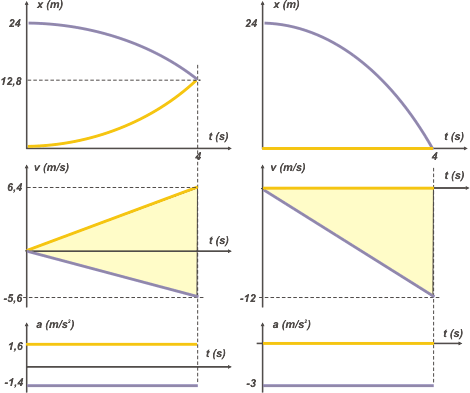
| Let´s take a look at the graphs. I´ll set up two columns. The one on the left will show the same graphs we have on the exercise 3.12, in which both rams were seen from land. The one on the right will show the universe as seen from the white ram´s frame of reference. |
|
|
 |
|
|
If you take a closer look, there´s a lot to take in, areas that are the same, differences between magnitudes that are actually the same, etc, etc. Get inspired. |
|
 |
| CHALLENGE: same problem than the one in 3.12 (the black ram starts running wrecklessly) but 1 second after the white one. |
|
| Some rights reserved. Reproduction allowe by quoting the source. Translated by Tomás de Udaetai. Last Updated jul-18. Buenos Aires, Argentina. |
|
|
| | |
|
|