NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Movimiento uniforme)
|
|

|
| |
FIS c5.05 - Una pelota es lanzada desde el piso con una
velocidad cuyo módulo es v0, formando un ángulo
α con la horizontal.
Despreciando el rozamiento con el aire:
a) Elegir un sistema de referencia y obtener las
expresiones de los vectores posición, velocidad y
aceleración en función del tiempo si v0= 5 m/s y
para los casos donde α = n . π/8 (n = 1, 2, 3, 4, 5).
b) Hacer los gráficos de posición y velocidad
en función del tiempo para los 5 valores de n.
c) Calcular la altura máxima y el alcance
para cada valor de n y graficar altura máxima vs n y A vs n. Interpretar. |
|
Sí, ya sé... no te gustan los ejercicios kilométricos, a mí tampoco. Pero es lo que hay.
Si era cortito jugamos un poco, pero si es tan largo hagámoslo sencillo y elijamos un sistema de referencia con t0 = 0, x0 = 0, y0 = 0, eje vertical hacia arriba.
Y arranquemos por aclarar ese geroglífico de los ángulos de disparo. Acordate que π representa un ángulo (en sistema radial) de 180 grados. De modo que π/8 es lo mismo que 22,5°. Por lo que tendremos cinco movimientos diferentes cada uno con una elevación de tiro diferente: α1 = 22,5°, α2 = 45°, α3 = 67,5°, α4 = 90°, α5 = 112,5°.
Mirá el esquemita (es solo un esquema, no representé el valor exacto de los ángulos): |
|
|
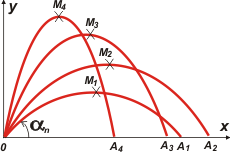 |
Con esto se te aclara el panorama. A medida que cambia el ángulo de tiro, cambia el alcance A, y cambia la altura máxima, M.
Los subíndices nos van a indicar la correspondencia entre los valores. (Si sos de los que tienen ese extraño complejo que no puede utilizar subíndices, largá la ciencia y dedicate a la floricultura). |
|
|
|
Vamos a las expresiones, como cualquier tiro oblicuo:
x = 5 m/s cos α t
y = 5 m/s sen α t – 5 m/s² t²
vx = 5 m/s cos α
vy = 5 m/s sen α – 10 m/s² t
ax = 0 m/s²
ax = – 10 m/s²
Vamos con el ítem c) y dejamos los gráficos para el final. Para calcular la altura máxima, M y el alcance, A para cada tiro podemos usar dos estrategias. La primera es la que ya conocés, le pedís a las ecuaciones que hablen de esos puntos y resolvés. La segunda es hallar una expresión genérica que te permita calcularlos en un solo paso. Esta opción, por principios, no debería enseñártela, pero en aras de la brevedad...
Hallemos la expresión de la altura máxima. Acordate que ahí la velocidad vertical se anula.
0 = 5 m/s sen α – 10 m/s² tM
10 m/s² tM = 5 m/s sen α
tM = 0,5 sen α s
Eso lo metemos en la ecuación de alturas:
y = 5 m/s sen α tM – 5 m/s² tM²
yM = 5 m/s sen α . 0,5 sen α s – 5 m/s² . (0,5 sen α s)²
yM = 2,5 m sen² α – 1,25 m sen² α
yM = 1,25 m sen² α
Para calcular el alcance hacemos algo parecido. Acordate que en el alcance la altura vale cero.
0 m = 5 m/s sen α tA – 5 m/s² tA²
5 m/s² tA² = 5 m/s sen α tA
5 m/s² tA = 5 m/s sen α
tA = sen α s
Eso lo metemos en la de posiciones horizontales:
xA = 5 m/s cos α tA
xA = 5 m cos α sen α
Y nos acordamos de lo que le respondió Euclides a su esposa cuando lo echó de la casa:
cos α sen α = ½ sen 2α
De donde:
xA = 2,5 m . sen 2α
Hagamos lo cálculos para cada uno de los ángulos que pide el ejercicio: |
|
|
| n |
α (en rad) |
α (en grados) |
xA (alcance, en m) |
yM (alt. máx., en m) |
| 1 |
π/8 |
22,5 |
1,77 |
0,183 |
| 2 |
π/4 |
45 |
2,50 |
0,625 |
| 3 |
3π/8 |
67,5 |
1,77 |
1,066 |
| 4 |
π/2 |
90 |
0 |
1,250 |
| 5 |
5π/8 |
112,5 |
–1,77 |
1,066 |
|
|
|
Como ves el alcance tiene un valor máximo ( que es este caso coincide con el ángulo de 45 grados). Bueno, eso ocurre siempre y se ve claramente en la expresión de alcance, ya que la expresión sen 2α que a lo sumo vale 1, alcanza ese valor cuando α vale 45°. En cambio la altura máxima se alcanza cuando la pelota se arroja verticalmente.
Resulta interesante hallar una expresión general para todo tiro oblicuo que se dispara a cualquier velocidad, v0, y llega al mismo nivel. Se arriba a estas expresiones de la misma manera en que lo desarrollamos acá pero en lugar de escribir 5 m/s, escribís v0. Y si no tenés ganas de gastar tinta lo podés ver en este otro ejercicio.
Los resultados a los que se arriba son éstos:
altura máxima yM = v0² sen² α / 2g
alcance máximo XA = v0² sen 2α / g
Por favor, fijate que incluye a nuestro caso de recién.
Con la tabla de valores que te hice allá arriba podés construir los gráficos que te piden. No dejes de hacerlo porque el análisis es muy rico. Y si sos un nerd hasta podés llegar al concepto de envolvente. |
|
|
| |
|
|
Desafío: ¿Cómo se llama la curva envovente de todas las trayectorias posibles con la misma velocidad inicial y diferentes ángulos? |
|
 |
| |
|
| Algunos derechos reservados.
Se prohibe estrictamente leer este ejercicio resuelto por encima: hay que leerlo despacio y con atención. Las penalizaciones a esta infracción son severísimas. Se permite su reproducción citando la fuente. Agradezco a Karen Calvo por el envío de una errata. Última actualización mar-16. Buenos Aires, Argentina. |
|
|
| |
|

