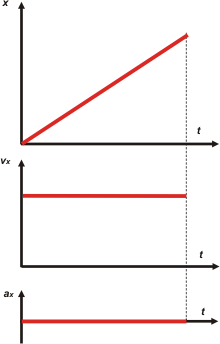
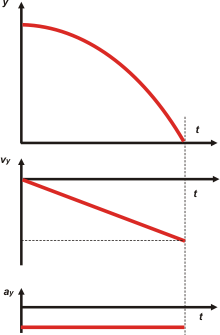
|
NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA
(Tiro oblicuo)

|
|

|
| |
 |
FIS c5.03 - Susana arroja horizontalmente su llavero desde la ventana de su departamento, y Andrés lo recibe a 1,2 m de altura sobre el piso, 0,8 segundos después. Sabiendo que Andrés se encuentra a 4,8 m del frente de la casa de Susana, hallar:
a - A qué altura del piso partió el llavero.
b - Con qué velocidad llegó a las manos de Andrés.
c - Cuál es la ecuación de la trayectoria. |
|
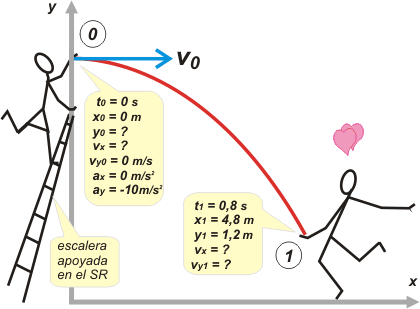
Repasemos cómo se hace un esquema: 1) dibujo la trayectoria; 2) indico en la trayectoria los puntos (o, si querés: eventos) de interés, ya sea porque contienen datos o porque contienen incógnitas que son preguntadas en el problema; 3) LES PONGO NOMBRE; 4) automáticamente surge el nombre de cada instante, posición, velocidad y aceleración (las características cinemáticas) de cada punto; 5) a cada característica le pongo el valor que corresponde, ya sea por ELECCION o por obligación. El SR quedó automáticamente determinado. Mirá el que hice yo: |
|
|
|
Luego escribimos las ecuaciones horarias. Para eso basta con reemplazar las constantes (to , xo , yo , vx , voy , y g) de las ecuaciones generales de cada movimiento (horizontalmente un MRU y verticalmente un MRUV), por las constantes iniciales de nuestro movimiento. Estos son los modelos, los de todo tiro oblicuo: |
 |
x = xo + vx ( t – to )
|
|
y = yo + voy ( t – to ) + ½ g ( t – to )²
|
|
vy = voy+ g ( t – to )
|
|
Y estas ecuaciones son las del llavero de Susana, que se obtienen al reemplazar las constantes (to , xo , yo , vx , voy , y g) que, fijate, están todas en el globito del esquema, al lado del punto 0. |
|
x = vx . t
y = yo – 5 m/s² . t²
vy = – 10 m/s² . t
|
| Estas son las ecuaciones que describen TODO el movimiento del llavero de la felicidad. |
|
Fijate que lo que acabo de escribir son las ecuaciones que describen TODO el movimiento del llavero; hablan de las infinitas posiciones que ocupa, y de sus respectivos instantes de tiempo. ¿OK?
El resto es automático: les pedimos a las ecuaciones que "hablen" de los puntos (como diría un físico: las especializamos) que tienen interés, en este caso sólo el punto 1. |
|
 |
|
 |
 |
4,8 m = vx . 0,8 s |
[1] |
|
| 1,2 m = yo – 5 m/s² . (0,8 s)² |
[2] |
|
| vy1 = – 10 m/s² . 0,8 s |
[3] |
|
|
|
| Estas son las ecuaciones especializadas para el instante que a Andrés y a vos les interesan. |
|
Inevitablemente desembocamos en un sistema de tantas ecuaciones como incógnitas. Lo que sigue es álgebra. Quede claro que acá terminó la física del problema. Igual te lo resuelvo: para eso están los NO ME SALEN. |
|
| De la ecuación [1] despejamos vx y calculamos |
|
| |
vx = 6 m/s |
|
|
| De la ecuación [2], despejando, sale directamente yo, que es una de las cosas que pide el enunciado del problema: la altura de la que parte el llavero. |
|
| |
yo = 4,4 m |
 |
|
|
| Ahora, de la ecuación [3], también sale directamente vy1 |
|
| |
vy1= – 8 m/s |
|
|
|
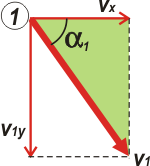
| Para saber con qué velocidad llega el llavero a manos de Andrés, hay que componer las velocidades horizontal y vertical en ese instante. Pitágoras lo hace por nosotros. |
|
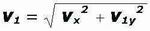 |
 |
|
|
| |
|
| |
v1 = 10 m/s |
|
|
El toque de distinción lo das indicando con qué ángulo llega el llavero a manos de Andrés. α1, respecto a la horizontal, es aquel cuya tangente vale vy1/vx. De modo que |
|
α1 = arc tg (vy1 / vx) = arc tg (– 8 m/s / 6 m/s) = arc tg (– 4/3)
α1 = – 53°
|
| No dejes para el día del examen aprender a usar la calculadora. |
|
| La ecuación de la trayectoria consiste en relacionar la altura con la posición de avance, y con x, y podemos obtenerla fácilmente, ya que contamos con una ecuación de y y una de x que dependen de la misma variable, t. Despejemos t de una de ellas y reemplacémosla en la otra. Mirá: |
|
| |
x = 6 m/s . t |
|
|
|
| entonces |
|
| |
t = x / 6 m/s |
|
|
|
| esta expresión de t la meto en la ecuación de alturas, y = 4,4 m – 5 m/s² . t² |
|
| |
| y = 4,4 m – |
|
0,139 |
. |
x ² |
|
| m |
|
|
|
|
|
|