| home | | | más de cinemática | | | otros temas de Física | | | lecciones del maestro Ciruela | | | tonterías | | | @ |
|
||||||||||||||||
|
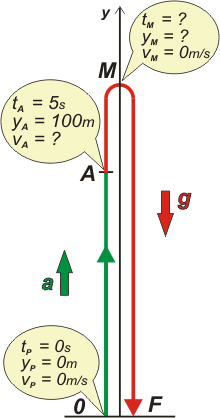
Como el movimiento es vertical y la cañita sube y baja por la misma recta, se me superponían puntos de la trayectoria dificultando la comprensión, así que separé la subida de la bajada aunque en realidad esto no ocurre. Detecté que en el enunciado se mencionaban cuatro puntos o situaciones diferentes y las ubiqué en la trayectoria poniéndoles nombres. A la partida la llamé 0, al punto en que se agota el combustible lo llamé A, al punto donde alcanza la altura máxima M, y cuando llega al piso F. (Qué original). Hasta que se agota el combustible, ¿qué tipo de movimiento es? Un MRUV sencillo y cualunque como cualquier otro. Con una aceleración constante que no sabemos cuánto vale, pero valga lo que valga... eso valdrá; acá g no tiene nada que opinar. Hay muchos estudiantes que piensan que la gravedad es una condición omnipresente, cuando simplemente es una característica cinemática que describe cómo varía la velocidad. Mientras la cañita está empujada por su propio motor a chorro va aumentando su velocidad con una aceleración, a, que lo único que hace es describir ese aumento. Después de que se agota el combustible -desde A en adelante- se trata de otro MRUV, este sí con una aceleración igual a g, y continúa así... subiendo y bajando hasta tocar el piso. |
|
Y cuántas ecuaciones describirán todo este movimiento. Cuatro, porsu, ya que hay dos movimientos variados y cada movimiento variado se describe con dos ecuaciones: una de posición y otra de velocidad. Esto es como llenar un formulario impreso; tomo los "modelos" de ecuación horaria... ¿los tenés a mano? Son estos: |
||
|
||
Y ahora reemplazo las constantes (to , yo , vo y a) por los valores iniciales: para el primer movimiento las del punto 0, y para el segundo movimiento las del punto A. |
||
| tramo con combustible |
y = ½ a. t² | Estas son las ecuaciones que describen TODO el fenómeno del movimiento contado en el enunciado. |
||
| v = a . t | ||||
| tramo libre (tiro vertical) |
y = 100 m + vA ( t – 5s ) – 5 m/s² . ( t – 5s )² | |||
| v = vA – 10 m/s² . ( t – 5s ) | ||||
Y ahora que tenemos las ecuaciones horarias, ellas solas resolverán el problema. Pidámosles que "hablen" de aquellos puntos de los que pueden decir algo interesante. O sea: usémoslas. A las dos primeras, que hablen del punto A; y a las dos del movimiento libre (¿por qué se llamará "libre"?), que hablen del punto M. A ver qué pasa... |
||||
| 100 m = ½ a . 25 s ² | [1] | Estas, en cambio, son las ecuaciones especializadas para los instantes que a vos te interesan. | ||
| vA = a . 5 s | [2] | |||
| yM = 100 m + vA ( tM – 5s ) – 5 m/s² . ( tM – 5s )² | [3] | |||
| 0 m/s = vA – 10 m/s² . ( tM – 5s ) | [4] | |||
| Me lo temía... un sistema de tantas ecuaciones como incógnitas. En este caso 4x4, pero muy pero muy fácil. Mirá: de la ecuación [1] despejamos a y calculamos: | ||||
| a = 8 m/s² | ||||
| esto lo reemplazo en la ecuación [2] y obtengo | ||||
| vA = 40 m/s | ||||
| Ahora, de la ecuación [4] despejo tM | ||||
| tM = 9 s | ||||
| con estos resultados voy a la última ecuación que queda, la [3] | ||||
| yM = 180 m | ||||
La velocidad vA es la máxima de todo el ascenso, la que nos pide el enunciado, ya que hasta allí fue aumentando, y desde allí irá disminuyendo, frenando hasta alcanzar la altura máxima. Ah, me olvidaba de los gráficos. Hacelos siempre como yo, en este orden, encolumnados y con la misma escala de tiempo. Así les decimos: "en tándem"... ¿Tendrá alguna ventaja hacerlo de este modo? |
||||
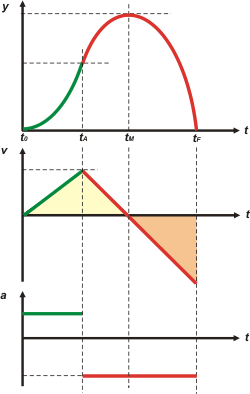 |
Usé el mismo código de colores que usé en el esquema: verde para el movimiento con motor y rojo para el libre. Fijate la tangente (la inclinación) de la curva en el instante tM. ¿Cuánto vale? |
||||
Animate a decirme sin hacer cuentas, cuál de las dos áreas es mayor, ¿la amarilla o la naranja? Mirá esto otro: la inclinación de la gráfica de velocidad, de 0 a A, es una inclinación (pendiente, como le gusta a los físicos) positiva; a partir de A, es una pendiente negativa... ¡que no cambia en el instante M! Ahora saltá al gráfico de aceleración y decime si no describe perfectamente la discusión que acabamos de hacer en el párrafo anterior. |
|||||
NOTA: vF, la velocidad con la que llega al piso, ¡no es cero! De hecho llega al piso con la mayor rapidez de todo el movimiento. |
|||||
| DESAFIO: Hallar tF y vF. Hallar en qué instantes la altura de la cañita vale 50 m, en qué instantes vale 120 m, y en cuál 200 m. Si aceptás el desafío hacelo íntegro, ya que -aunque lo parece- NO es reiterativo: cada una de las alturas implica una dificultad diferente. |  |
||||
|
|||||